这里放些字符串相关，总之也就是从头再学字符串了。
基本概念
border：一个字符串的真前缀，并且它和该字符串的一个真后缀相等。
周期：对于字符串 $s$ 和一个整数 $0 < p \le |s|$，$\forall i, s[i]=s[i+p]$，则 $p$ 为字符串 $s$ 的周期。可以证明，一个字符串的周期等于该字符串的长度减去它的最长 border 的长度。
$lcp(a, b)$：$a$ 串和 $b$ 串的最长公共前缀。
$lcs(a, b)$：$a$ 串和 $b$ 串的最长公共后缀。
字符串哈希
比较简单基础的算法，但是用处够多。
具体实现不说了，应该都会。主要可以用来在忘了 SA 板子怎么写后去 $O(\log n)$ 的求 lcp 和 lcs，或者是 $O(1)$ 判定字符串相等。
KMP
KMP 是用来求解一个字符串的所有前缀的最长 border 的算法。具体算法流程如下：
我们定义 $next[i]$ 为该字符串长度为 $i$ 的前缀的最长 border 长度。显然，$next[1]=0$。我们考虑如何用已知的 $next[i]$ 计算后面的 $next$。
我们可以结合下面的图来理解：
图中我们发现 $i-1$ 的 border 无法匹配上第 $i$ 个位置，我们就再跳到 border 的 border。由图可以看到，border 的 border 还是原串的 border。我们就可以不断跳 border 直到匹配上第 $i$ 位。
代码如下：
1 | ne[1] = 0; |
由于每轮循环 $j$ 至多 $+1$，而每次跳 border 至少会让 $j$ 减一，因此内层循环不会执行超过 $m$ 次。总复杂度即为 $O(|s|)$。
例题后面有。
exKMP（z 函数）
exKMP 和 KMP 相似，但是它是用来求字符串的前缀和该字符串的某个后缀的最长匹配长度。可以想象成这个字符串往后平移，平移到某个位置后从这个字符串开头进行匹配。
在 exKMP 中，我们有一个数组 $z_i$，表示该字符串的前缀和第 $i$ 个后缀（也就是 $[i, |s|]$ 这段区间）的最大匹配长度。我们考虑如何快速求出 $z_i$。
首先，显然的是 $z_1=|s|$，因为它自己和它自己匹配必定长度为 $|s|$，但是我们不能用这个条件，否则就没用了。我们考虑维护一个连续段，这个连续段和该字符串的前缀能够完全匹配。当现在要求的位置在连续段之外，我们只能暴力往后跑。而在连续段之内时，我们可以利用最开头的 $z$ 值来加速递推。而当顶到连续段的边界时，我们依旧只能暴力求解。
代码如下：
1 | inline void getz(char *s, int n) |
由于每次 while 循环至少使得 $r$ 加一，而 $r \le n$。因此内层循环的次数不会超过 $n$ 次。总复杂度 $O(|s|)$。
manacher
manacher 算法是用来快速求解字符串中回文串的算法。具体算法流程如下：
我们先对字符串进行预处理，在左右两边加入哨兵，再在每两个字符之间加入一个相同的且在原串中不存在的字符，来使得偶回文串变为奇回文串。我们再设 $f_i$ 为以 $i$ 位置为中心的最长回文半径。类似于 exKMP，我们也可以维护一个相同的段，只不过这次我们要维护的是一个右端点最靠右的最长回文段。在这段之外就暴力，之内就利用之前的信息，然后再暴力扩展。
代码如下：
1 | inline void manacher(char *t) |
时间复杂度分析同 exKMP。
Trie
没啥可说的，就只是单纯的字典树。
对于异或问题基本上要么想拆位，要么线性基，要么应该就是 01 Trie 了。
注意 01 Trie 的空间复杂度为 $O(n\log n)$。如果空间限制比较紧并且只用到一次把整棵树遍历一遍可以考虑滚动数组 Trie。
可持久化 Trie 和主席树差不多，基本上都是维护前缀的信息用的，只不过可持久化 Trie 一般是维护异或信息的。
AC 自动机
AC 自动机和 KMP 类似，都是求解字符串匹配的问题，但是 AC 自动机可以支持多模式串对一个文本串进行匹配，时间复杂度同样也是线性。
AC 自动机一开始可以看作一颗 trie 树。在 AC 自动机中，我们类似 KMP，我们维护一个 $fail$ 指针，表示与后缀能够匹配的最长前缀所在的节点编号。不过这个 $fail$ 指针可能指向别的字符串中的位置，但是这无关紧要，我们做的是多模式串匹配。
对于求 $fail$ 指针，我们可以采取 bfs 的方法。因为类似 KMP，我们所有的信息都是从前面递推过来的，因此我们只要知道所有深度小于当前节点的信息，我们就可以递推出来。我们也可以类似 KMP，一直跳 $fail$ 指针，直到匹配或者跑到根节点。而对于匹配文本串也是一样。
在 AC 自动机中，我们可以对 $fail$ 指针做一个优化。因为每个节点有 $26$ 个儿子，而这些儿子大部分都没有被创建出来，我们考虑利用一下这些空数组，我们定义 $tr[p][u]$ 为节点 $p$ 假设有 $u$ 这个儿子，这个儿子的 $fail$ 指针指向的位置，这个也可以递推得到。这样我们就不用每次跳 $fail$ 了。
代码如下
1 | inline void insert(char *s, int ident) |
代码来源于AC 自动机（二次加强版）。我们可以注意到，在查询出现次数时，我们为了优化复杂度，利用了树上差分的思想，某个点如果出现过，那么它 $fail$ 指针和 $fail$ 的 $fail$ 也会出现。因为我们从大到小枚举节点编号，也就是 trie 树从下而上的拓扑序。直接拓扑排序的时候加上即可。
PAM（回文自动机）
PAM 中有两棵树，分别对应着字符串中的奇回文串和偶回文串。而 PAM 中的 $fail$ 指针和 AC 自动机中相似，设 $fail_x$ 为 $x$ 代表的回文串的最长回文后缀所对应的节点。这个 $fail$ 指针有利于我们插入节点。
当我们要新加入一个字符时，它可能会和原字符串中的末尾形成一个回文串。由于是回文串，因此两边同时扣掉一个字符依旧是回文串。我们发现这个回文串也就是一个回文后缀。我们直接在这个回文后缀所对应的节点后挂上这个节点即可。这个过程就可以用 $fail$ 指针来做。
关键结论：$s$ 的回文后缀按长度排序后会形成 $\log |s|$ 段等差数列，可以考虑把信息记录到等差数列顶。
建树代码：
1 | inline int getfail(int x, int i) |
SA（后缀数组）
SA 是一个把所有后缀都放到一个数组，支持动态查询一个后缀的排名的结构。在其中有两个重要数组：$sa_i$ 和 $rk_i$。$sa_i$ 表示排名第 $i$ 的后缀为哪个，$rk_i$ 表示第 $i$ 个后缀的排名。
有一个很简单的构建方法就是把所有后缀都搂出来然后 sort 一下。但是字符串比较是 $O(n)$ 的，因此这样的复杂度是 $O(n^2\log n)$。我们可以利用倍增，用上一层的 $rk_i$ 来为下一层做准备。下面放一张图来理解：
每次只会对两个关键字进行比较。我们可以简单粗暴用 sort，时间复杂度 $O(n\log^2 n)$，但是为了少一个 $\log$，我们可以用基数排序，这样时间复杂度即为 $O(n\log n)$。
构建代码
1 | m = 127; |
我们还可以求出一个数组 $height_i$，表示 $lcp(sa_i, sa_{i-1})$。有一个引理：$height[rk[i]] \ge height[rk[i-1]]-1$，这样我们就可以直接暴力求了。
对于 $height$ 数组，有这样一个用处：$lcp(sa[i], sa[j])=\min {height[i + 1]\cdots height_{j} }$。这样就可以把 $lcp$ 转化为 RMQ 问题来处理了。
SAM（后缀自动机）
SAM 是一张 DAG，存储了一个字符串的所有子串。我们必然不能把后缀一个一个插入 trie 树里面当 SAM 用，但是我们可以利用 parent tree 来构建。
parent tree 是利用了字符串的子串的 $endpos$ 来构建起来的。我们可以用 parent tree 的结构来建立我们的 SAM，SAM 中的每个节点都是在 parent tree 上的。
SAM 的具体构建这里不细说了，但是 SAM 中的后缀链接（即 $link[x]$），表示它在 parent tree 中的父亲。
（这里是真的不想写了要细写估计得再开一篇博客写）
注意：SAM 的节点数最多为 $2n-1$ 个，转移最多有 $3n-4$ 个。
构建代码如下：
1 | inline void extend(char *s) |
后缀平衡树
点击查看
我不会，以后再学习
一些题目
Matching
对于整数序列 $(a_1,a_2,\cdots,a_n)$ 和 $1\sim n$ 的排列 $(p_1,p_2,\cdots,p_n)$，称 $(a_1,a_2,\cdots,a_n)$ 符合 $(p_1,p_2,\cdots,p_n)$，当且仅当：
${a}$ 中任意两个数字互不相同；
将 $(a_1,a_2,\cdots,a_n)$ 从小到大排序后，将会得到 $(a_{p_1},a_{p_2},\cdots,a_{p_n})$。
现在给出 $1\sim n$ 的排列 ${p}$ 和序列 $h_1,h_2,\cdots,h_m$，请你求出哪些 ${h}$ 的子串符合排列 ${p}$。
数据范围：$n, m\le 1000000$。
KMP 好题。我们考虑将判定相等转化一下，可以变为：在它之前比它小的数的个数。这个映射很容易证明是和原来的序列一一对应的。因此我们可以用这个条件来判定相等。我们先预处理出来 $p$ 中的这个值，记为 $cnt_i$。然后由于要求匹配，我们可以用 $KMP$。查询小于它的数可以直接用树状数组来做。
时间复杂度 $O(n\log n)$。
Fedya the Potter Strikes Back
给定一个字符串 $S$ 和一个序列 $W$，初始时它们都为空。你需要在线完成 $n$ 次操作。每次操作在 $S$ 后面添加一个字符 $c_i$，在序列 $W$ 后面添加一个数字 $w_i$。
定义一个子区间 $[L, R]$ 的可疑度为：若子串 $[L,R]$ 和前缀 $[1,R-L+1]$ 相同，则其可疑度为 $\min_{i=L}^{R} W_i$。否则其可疑度为 $0$。
每次操作后，你都要求出当前的串的所有子区间的可疑度之和。
数据范围：$1\leq n\leq 6\times 10 ^ 5$，$0\leq w_i < 2^{30}$。
我们考虑维护 Border 的集合。我们发现，新加入一个字符至多会在上一个的基础上增加一个 Border，因此我们直接删的复杂度是对的。
具体地说，我们维护一个 $anc_i$，表示在 $fail$ 树上 $i$ 的祖先中第一个和 $i$ 后继字符不同的节点。这样就能快速找到要删除的 Border。
至于权值的问题，我们发现小的值会覆盖掉大的值，因此我们使用单调栈，同时我们将大于 $w_i$ 的权值全部设为 $w_i$。这样的复杂度也是均摊 $O(\log n)$ 的。因此总复杂度为 $O(n\log n)$。
字符串匹配
定义 $A^1=A$，$A^n = A^{n - 1} A$（$n \ge 2$ 且为正整数）。求 $S = {(AB)}^iC$ 的方案数，其中 $F(A) \le F(C)$，$F(S)$ 表示字符串 $S$ 中出现奇数次的字符的数量。两种方案不同当且仅当拆分出的 $A$、$B$、$C$ 中有至少一个字符串不同。
数据范围：$|S|\le 10^6$。
终于有 exkmp 可做的题了。
我们先不考虑 $F(A) \le F(C)$ 的限制。我们现在先枚举循环的长度，我们现在要找出有多少循环（这时我们先把 $A$ 和 $B$ 看作整体）。我们考虑用 exkmp 来求。
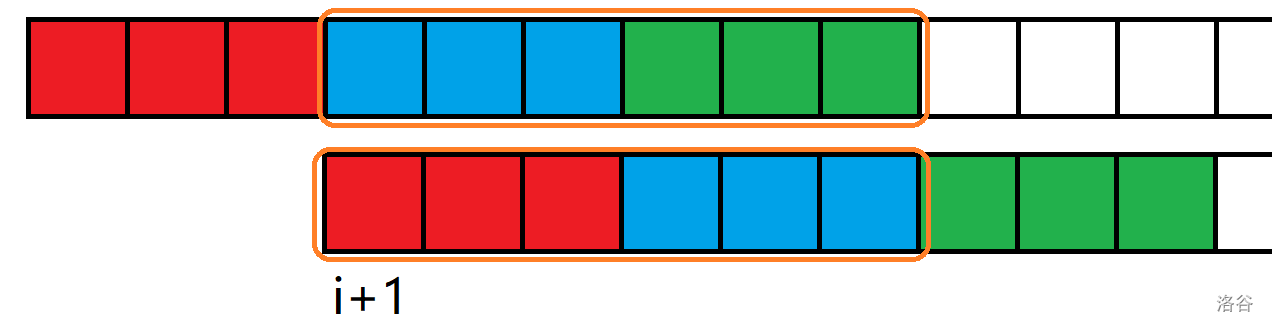
我们先把原字符串和原字符串的第 $i + 1$ 位对齐。见下图：
我们可以清楚的看到相同颜色部分是相同的，框起来的部分也是相同的。手玩下就能得到当循环长度为 $i$ 时循环的个数为 $\left \lfloor \frac{z[i+1]}{i} \right \rfloor +1$。
现在我们加上 $F$ 的限制，我们考虑分情况讨论。我们将前缀分为由奇数个循环拼成和偶数个循环拼成。假设一共有 $t$ 个循环，那么显然由奇数个循环拼成的前缀有 $t - \left \lfloor \frac{t}{2} \right \rfloor$，偶数个的前缀有 $\left \lfloor \frac{t}{2} \right \rfloor$ 个。我们下面来分类讨论。
当有奇数个循环时，我们考虑剩下的后缀的字母奇偶性都是等价的。因为我们加入两个循环时字符的奇偶性必然不会改变。因此我们维护单个变量 $suf_i$ 维护 $s[i\sim n]$ 的奇数字符的个数，同时维护 $pre_i$ 为 $s[1\sim i]$ 的奇数字符的个数。我们找符合要求的奇数循环个数时我们只需要寻找有多少前缀 $j$ 满足 $pre_j\le suf_i$（$i$ 为枚举的循环长度）。
而对于偶数个循环时同理，只不过 $C$ 的字母奇偶性和整个字符串相同。因此我们依旧维护 $pre_i$，我们只要寻找有多少前缀 $j$ 满足 $pre_j\le all$ 即可。而对于前缀查询，直接树状数组即可。
时间复杂度 $O(n\log 26)$。
Prefix-Suffix Palindrome
给定一个字符串。要求选取他的一个前缀（可以为空）和与该前缀不相交的一个后缀（可以为空）拼接成回文串，且该回文串长度最大。求该最大长度。
数据范围：$\sum n\leq 10^6$ 。
我们考虑如何拼接才是最大的。显然，我们先选取最长逆序相等的前后缀，然后再找一个和这个前后缀相交的回文串即可。如何求这个最长逆序相等的前后缀呢，我们可以把字符串反转后拼到原串后，跑一遍 exKMP，$z_{n+1}$ 即为所求，然后再对整个串跑马拉车，之后枚举每个位置能否拼上这个前缀或后缀即可。
最长双回文串
输入长度为 $n$ 的串 $S$，求 $S$ 的最长双回文子串 $T$，即可将 $T$ 分为两部分 $X, Y$（$|X|,|Y|≥1$）且 $X$ 和 $Y$ 都是回文串。
数据范围：$2\leq |S|\leq 10^5$。
我们先对原串跑一遍马拉车，求出每个点所对应的最长回文半径，然后从后往前递推出一个数组 $maxl_i$，表示 $i$ 为最左端的回文串的最长长度。然后枚举每个点，看最长能拼成多长的双回文串。
动物园
给定字符串 $s$，设 $num[i]$ 为对于 $s$ 前 $i$ 个字符构成的字符串，长度不大于 $\left \lfloor \frac{i}{2} \right \rfloor$ 的 border 的数量。求出所有 $num[i]+1$ 的乘积。
数据范围：$|s|\le 10^6$。
我们考虑暴力：我们对于每个点暴力跳 $next$，这样就能统计出所有的 $num$。但是如果字符串所有的字符都相同就寄了。因此我们考虑用前面的数据加速一下。
因为 border 的 border 也是 border，因此我们可以得到一个结论：$num[i]=num[j]+1$，其中 $j$ 为 $1\sim i$ 第一个不超过 $\left \lfloor \frac{i}{2} \right \rfloor$ 的 border。根据这个我们就可以加速递推了。我们维护一个大小始终不超过 $\left \lfloor \frac{i}{2} \right \rfloor$ 的指针 $j$，依旧按照 kmp 的思路找 border，一旦发现超过了 $\left \lfloor \frac{i}{2} \right \rfloor$ 就跳 $next$，直到满足条件然后更新即可。
时间复杂度 $O(n)$。
优秀的拆分
如果一个字符串可以被拆分为 $\text{AABB}$ 的形式，其中 $\text{A}$ 和 $\text{B}$ 是任意非空字符串，则我们称该字符串的这种拆分是优秀的。现在给出一个长度为 $n$ 的字符串 $S$，我们需要求出，在它所有子串的所有拆分方式中，优秀拆分的总个数。
数据范围：$n\le 30000$。
我们考虑将 $A$ 部和 $B$ 部分开，我们设 $f_i$ 为 $i$ 位置从左有多少方案可以拼成 $\text{AA}$，设 $g_i$ 为从 $i$ 位置往右有多少方案可以拼成 $\text{BB}$。则最终答案即为 $\sum f_i\times g_{i+1}$。
我们考虑如何求出 $f_i$，$g_i$ 则同理。我们先枚举 $\text{A}$ 的长度，我们每隔 $k$ 个位置建立一个检查点，那么这个 $\text{AA}$ 一定会经过两个检查点，可以见下图：
我们只需要考虑两个相邻检查点往前的 $lcs$ 和往后的 $lcp$，看一下是否能重合上即可。而重合部分是我们可以自由调整的，我们就把一段区间的 $f$ 都增加 $1$ 即可，用差分维护。
时间复杂度 $O(n\log n)$。
所有公共子序列问题
给定两个字符串 $A, B$，求出 $A$ 和 $B$ 所有本质不同的公共子序列的数量。
数据范围：$|A|,|B|\le 3000$。
本题介绍一种新自动机：子序列自动机。具体的说，给定字符串 $s$，我们设 $ne[i][c]$ 为 $i$ 点之后第一个字符 $c$ 出现的位置。构建直接从后往前扫即可。
它的用处主要有：统计字符串不同子序列个数、查询一个字符串是否是该字符串的子序列、两个字符串的公共子序列、因此本题说是子序列自动机的板子题也可以其实。
回到这题，我们可以同时对两个字符串在两个子序列自动机上走，每次枚举下一个字符填什么，然后走就完事了。统计答案也可以像在 DAG 上统计一样，DP 或者记忆化即可。
残缺的字符串
给定两个字符串 $A, B$，两个字符串中都可能出现通配符 *，表示这个位置可以为任意一个字符。求出对于 $B$ 的每个位置 $i$，从这个位置开始连续 $m$ 个字符形成的子串能否和 $A$ 成功匹配。
数据范围：$|A|, |B| \le 3\times 10^5$。
这里介绍一个新东西：FFT 求字符串匹配。
先考虑没有通配符的情况，我们将每个位置附一个权值，那么两个字符串 $a, b$ 从 $1$ 开始匹配，成功匹配的条件即为：$\sum \limits_{i=0}^{m-1} (a_i-b_i)^2$。
而对于有通配符的情况，我们可以把通配符的权值设置为 $0$，同时判定成功的条件改为：$\sum \limits_{i=0}^{m-1} (a_i-b_i)^2a_ib_i$。而对于每一个位置，我们写出的式子就是下面这个样子：
$$
\sum \limits {i=0}^{m-1}(a_i-b{i+k})^2a_ib_{i+k}
$$
展开即为差卷积形式，NTT 即可。
时间复杂度 $O(n\log n)$。
歌唱王国
给定字符集大小 $n$ 和一个长度为 $m$ 的字符串 $a$。每次随机生成一个字符集中的字符放到字符串 $b$ 后（$b$ 初始为空），当 $b$ 中出现 $a$ 的时候停止。求最终的期望长度。
数据范围：$n, |a|\le 10^7$。
我们设 $f_i$ 为长度为 $i$ 时停止的概率，$g_i$ 为长度为 $i$ 时未停止的概率。我们再写出这俩玩意的生成函数 $F(x)=\sum f_i x^i$ 和 $G(x)=\sum g_i x^i$。
根据定义，我们很容易能写出 $F(1)=1$，因为最终总会结束，因此和一定为 $1$。而我们要求的答案为 $F’(1)$，因为根据期望的定义，我们的答案就是 $\sum i\times f_i$。求导就可以得到这个系数的多项式。
接下来就是推式子时间：
显然的，$g_i=g_{i+1}+f_{i+1}$，因为未结束的时候再放字符要么结束要么不结束。比较系数可以得到这个式子：
$$
xG(x)+1=F(x)+G(x)
$$
接下来这个式子不是特别显然。我们考虑在没有结束的局面下强行在后面构造出来一个 $a$，那么这时一定会结束。但是在这个结束前可能会提前结束，见下图：
因此我们只需要枚举 $a$ 的 border 即可。这里我们前面还要构造出前面的那一部分 $a$，对齐系数后我们的式子就是：
$$
G(x)\times \left ( \frac{1}{n}x \right )^m=\sum \limits _{i=1}^{m}F(x)\times \left ( \frac{1}{n}x \right )^{m-i}[1\sim i \ is\ \text{border}]
$$
我们得到这两个式子后再推推。把上面那个式子两边求导，得到：
$$
F’(x)=xG’(x)-G’(x)+G(x)=(x-1)G’(x)+G(x)
$$
我们把 $x=1$ 带入即可得到 $F’(1)=G(1)$。再代入上面特别长的那个式子，可以得到：
$$
\begin{aligned}
G(1)\times \left ( \frac{1}{n} \right )^m & = \sum \limits _{i = 1}^{m}F(1)\times \left ( \frac{1}{n} \right )^{m-i}[1\sim i \ \text{is}\ \text{border}]\
G(1)&=\sum \limits _{i = 1}^{m}F(1)\times n^i[1\sim i \ \text{is}\ \text{border}]\
G(1)&=\sum \limits _{i = 1}^{m}n^i[1\sim i \ \text{is}\ \text{border}]
\end{aligned}
$$
直接 $O(n)$ 算即可。
Kefa and Watch
给定长度为 $n$ 的只包含 $0\sim 9$ 的字符串，两种操作：区间赋值、区间询问是否含有长度为 $d$ 的周期。
数据范围：$n\le 10^5$。
根据周期的定义，周期就等于长度减去它的 border 长度。因此我们只需要判断是否存在长度为 $len-d$ 的 border 即可。我们直接用线段树维护即可。
时间复杂度 $O(n\log n)$。
Yet Another LCP Problem
记 $lcp(i,j)$ 表示i这个后缀和j这个后缀的最长公共前缀长度。给定一个字符串，每次询问的时候给出两个正整数集合 $A$ 和 $B$，求 $\sum_{i \in A,j \in B}lcp(i,j)$ 的值
数据范围：$n\le 2\times 10^5, \sum |A|+|B| \le 2\times 10^5$。
我们先把字符串翻转，将 $lcp$ 转化为 $lcs$。根据[AHOI2013]差异的套路，我们建出来 SAM，这样两个点在 parent tree 上对应的 lca 的 $len$ 即为最长公共后缀。
但是这里有多组询问，我们就可以每组询问建虚树，然后在虚树上进行 dp 计算答案。具体的说，我们设 $sum_{u, 0}$ 为 $u$ 子树中 $A$ 集合点的数量，$sum_{u, 1}$ 为 $u$ 子树中 $B$ 集合点的数量。通过容斥我们就能算出有多少 $a\in A, b\in B$ 的 lca 是 $u$。最终再乘上 $len_u$ 即可。
时间复杂度 $O(n\log n)$。
Check Transcription
给定一个 $01$ 串 $t$ 和一个字母串 $s$，求有多少对字符串 $(r_0, r_1)$ 满足 $r_0 \neq r_1$ 且将 $t$ 中的 $0$ 都换成 $r_0$，$1$ 都换成 $r_1$ 后，得到的字符串与 $s$ 相同。
数据范围：$2 \leq |t| \leq 10^5$，$1 \leq |s| \leq 10^6$。
我们直接枚举第一位 0/1 的长度，这样我们就能得到它的哈希值，同时我们也能算出另一种字符串的长度（我们假设第一位为 $0$），那么我们可以扫一遍 $01$ 串来得到它的哈希值，直接比较是否和原串相同即可。
复杂度证明：
我们先设 $s_1$ 为原串，$s_2$ 为 01 串。$cnt_0$ 为 0 出现的个数，$cnt_1$ 同理。
我们一共会枚举 $\frac{|s1|}{cnt_0}$ 个 $len$。我们可以把 $cnt_0$ 和 $cnt_1$ 的方程列出来：
$$
cnt_0\times len_0 + cnt_1\times len_1=|s_1|
$$
根据 exgcd，我们可以得到 $len_0$ 会每间隔 $\frac{cnt_1}{\gcd(cnt_0, cnt_1)}$ 出现一次。因此最多会扫 $\frac{|s_1|\times \gcd(cnt_0, cnt_1)}{cnt_0\times cnt_1}$ 次。每次扫都是 $O(|s_2|)$ 的。因此总复杂度为：
$$
\frac{|s_2|\times |s_1|\times \gcd(cnt_0, cnt_1)}{cnt_0\times cnt_1}
$$
我们让所有 $cnt_0$ 相关变量取到上界即可得到最终复杂度：$O(|s_1|)$。
Two Permutations
给出两个排列 $a,b$，长度分别为 $n,m$，求有多少个 $x$， 使得 $a_1 + x,a_2 + x,…a_n + x$ 是 $b$ 的子序列。
数据范围：$n \leq m \leq 2 \times 10^5$
我们枚举 $x$，这时我们就可以算出 $b$ 中哪些数被加入到选择的集合中。我们使用平衡树来维护这个过程以及 $b$ 之间的相对位置关系，同时当 $a$ 全体增加 $x$ 时，$a$ 的哈希值是可以计算出来的。因此我们再对这颗平衡树上的点进行一个哈希。每次比较即可。
时间复杂度 $O(n\log n)$。
e-Government
维护一个字符串集合，支持三种操作：
- 加字符串
- 删字符串
- 查询集合中的所有字符串在给出的模板串中出现的次数
数据范围：$m \leq 3 \times 10^5, \sum |s_i| \leq 3\times 10^5$。
我们先考虑没有删除加入时如何做。我们先把所有字符串加进 Trie 里面，在建 AC 自动机的时候按照 fail 向下更新出现次数即可。而在跑匹配的时候我们只需要把经过的点的权值加入即可。
而对应添加和删除操作，我们思考下更新的本质。一个点的贡献会沿着它在 fail 树上的边向下一直传下去，而我们要消除这些贡献或者增加这些贡献，只需要将它在 fail 树中的子树全部减去它的贡献即可。因此我们再把 fail 树建出来，每次添加删除直接子树 $+1$ 或 $-1$ 即可。
时间复杂度 $O(\sum |s_i|\log n + |T|)$
String Set Queries
维护一个字符串集合，支持三种操作，强制在线：
- 加字符串
- 删字符串
- 查询集合中的所有字符串在给出的模板串中出现的次数
数据范围：$m \leq 3 \times 10^5, \sum |s_i| \leq 3\times 10^5$。
本题和上面的区别就是强制在线。
做法 1：
二进制分组。我们对每次插入的一个字符串建立一个 AC 自动机，而当两个 AC 自动机大小相等时我们把这两个 AC 自动机暴力合并重构。每次查询就在 $\log n$ 个 AC 自动机查询即可。而对于删除，我们可以注意到信息可减，因此我们可以对删除过的字符串再做一遍。
时间复杂度 $O(n\log n)$。
做法 2：
我们直接哈希。每次直接枚举字符串 $t$ 长度为 $|s_i|$ 的子串，暴力比较哈希即可。
时间复杂度 $O(n\sqrt n)$。因为我们要让匹配次数最多的话，字符串长度一定是：1 2 3 4 ...。这样最多会有 $\sqrt n$ 个字符串。因此每次询问为 $n\sqrt n$。
做法 3：
我们考虑根号分治。我们对于长度大于 $\sqrt n$ 的 $s_i$ 直接暴力跑 kmp 匹配。而对于长度小于 $\sqrt n$ 的字符串，我们把它们都放到 trie 树上，然后枚举 $t_i$ 的后缀去上 trie 上去匹配去。因为长度都小于 $\sqrt n$，因此树高也为 $\sqrt n$。复杂度 $O(n\sqrt n)$。
[NOI2018] 你的名字
给定一个字符串 $S$，多次询问。询问给定一个字符串 $T$，有多少 $T$ 的子串满足其不为 $S[l\sim r]$ 构成的字符串的子串。
数据范围：$|S|\le 5\times 10^5, \sum |T|\le 10^6$
我们先考虑 $L=1, R = |S|$ 的情况。这时我们对 $S$ 和 $T$ 分别建 SAM，对 $T$ 的第 $i$ 个前缀，我们要找出它最长的后缀且这个后缀是 $S$ 的子串。我们加入 $T$ 的第 $i$ 个字符后，我们看当前节点是否有这一个转移，如果没有就一直跳 $link$。
最后我们将每一个前缀的满足上面要求的最长后缀记录为 $lim_i$。我们再设 SAM 上第 $i$ 个节点对应字符串中的位置是 $tag_i$。那么最后的答案就是：
$$
\sum \limits_{p=1}^{idx}\max(0, \mathrm{len}(p)-\max(\mathrm{len}(\mathrm{link}(p)), lim_{tag_p}))
$$
也就是对于每个节点，我们用它的长度减去它匹配的长度就是它不为 $S$ 子串的长度。
而对于有了区间限制这个东西，我们可以思考一下我们上面用 SAM 都做了什么：跳 $link$ 和看是否有转移。我们可以直接用线段树维护每个点的 $\mathrm{endpos}$ 集合。当这个集合中有我们限制的区间之内的位置，我们才可以进行转移，否则就跳出了这个区间。
而对于 $\mathrm{endpos}$，在 parent tree 上是父亲包含儿子的关系，因此我们直接线段树合并维护一下就好了。
时间复杂度 $O(n\log n)$。
区间本质不同子串个数
给定一个长度为 $n$ 的字符串 $S$，$m$ 次询问由 $S$ 的第 $L$ 到第 $R$ 个字符组成的字符串包含多少个本质不同的子串。
数据范围：$n\le 10^5, m\le 2\times 10^5$。
对于区间数不同颜色这种问题，一个常见的套路为讲询问离线，然后右端点扫描线，同时只维护每个不同元素在最右端出现的位置。
而对于这题我们也可以这么做。我们把询问离线后做扫描线，发现每次新加入的元素的 $\mathrm{endpos}$ 都包含新加入的右端点，也就是都是以右端点为结尾的子串。可以发现这些字符串在 parent tree 上对应着到根的一条链，于是我们的任务就变成了把这条链上的原来的影响消除，并且把它们在新位置的贡献加上。
我们就可以沿用[SDOI2017] 树点涂色的套路，用 LCT 来维护这个过程。具体地说，我们在 LCT 的每个点维护一个 $val$，表示它目前 $\mathrm{endpos}$ 的最大值。每次 access 时我们把一整条链的影响全部消除，同时把最终这条实链的 $val$ 全部覆盖为当前的右端点。然后我们再把当前新增加的字符串的开始位置加上即可。
时间复杂度 $O(n\log^2n)$。