一种 dp 优化
前置知识
单调队列优化 dp,计算几何基础知识,小学数学。
斜率优化
在 dp 中,我们常常能遇到一类转移方程,其中含有 i 相关的项与 j 相关的项的乘积,形如这种形式:
fi=j<imax{fj+aibj}
我们常见的单调队列优化只能优化只含 j 项的方程,对于这种方程无能为力。因此我们需要利用斜率优化。
先来看一道例题:
任务安排
n 个任务排成一个序列在一台机器上等待完成(顺序不得改变),这 n 个任务被分成若干批,每批包含相邻的若干任务。
从零时刻开始,这些任务被分批加工,第 i 个任务单独完成所需的时间为 ti。在每批任务开始前,机器需要启动时间 s,而完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。
每个任务的费用是它的完成时刻乘以一个费用系数 ci。请确定一个分组方案,使得总费用最小。
数据范围:n≤5000,ti,ci>0。
加强版:n≤100000,ti,ci>0。
先设 sumT[i] 为 ti 的前缀和,sumC[i] 为 ci 的前缀和。
我们可以很容易设计出一个 O(n3) 的转移方程:设 f[i][j] 为前 i 个任务共分为 j 段的最小花费。我们就可以列出转移:
f[i][j]=k<imin{f[k][j−1]+(sumT[i]+j×s)×(sumC[i]−sumC[k])}
因为状态数为 O(n2) 级别,无论如何优化都无法通过加强版
因为时间复杂度太高,我们考虑重新设计状态。设 f[i] 为前 i 个任务分为若干段的最小花费,则
f[i]=j<imin{f[j]+sumT[i]×(sumC[i]−sumC[j])+s×(sumC[n]−sumC[j])}
这个方程运用了一个费用提前计算的思想,最后一项 s×(sumC[n]−sumC[j]) 表示虽然不知道后面分成了多少段,但是知道当前分这一段会对后面这些项造成这么多影响。这个方程的复杂度为 O(n2),可以通过原版数据范围。
为了通过加强版,我们化简一下式子。
f[i]=j<imin{f[j]+sumT[i]×(sumC[i]−sumC[j])+s×(sumC[n]−sumC[j])}=j<imin{f[j]+sumT[i]×sumC[i]−sumT[i]×sumC[j]+s×sumC[n]−s×sumC[j])}=j<imin{f[j]−(sumT[i]+s)×sumC[j])}+sumT[i]×sumC[i]+s×sumC[n]
我们移一下项,变为:
f[i]−sumT[i]×sumC[i]−s×sumC[n]=j<imin{f[j]−(sumT[i]+s)×sumC[j])}
这时就无法化简了,我们考虑下有什么性质。
我们可以设 xj=sumC[j],yj=f[j],ki=(sumT[i]+s),bi=f[i]−sumT[i]×sumC[i]−s×sumC[n]。(注意下标)这时式子变为:
bi=j<imin{yj−ki×xj}
这就变成了一个一次函数求截距的式子。注意到 sumT[i]×sumC[i]−s×sumC[n] 在 i 固定时为定值,目前要求 f[i] 最小值,则问题转化为求截距的最小值。
我们可以把问题放到坐标系中来看:
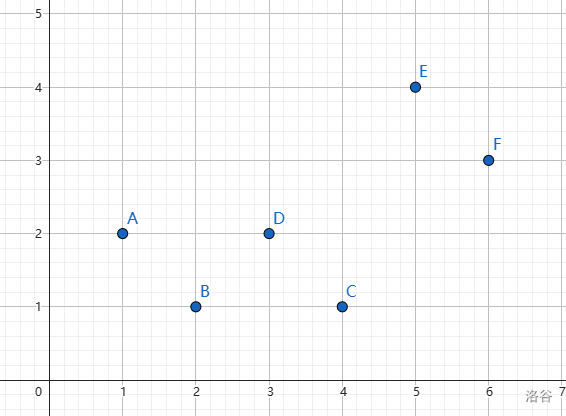
由于 i 固定,则斜率 ki 固定。我们就可以把问题想象成拿着一条斜率为 ki 的直线从下往上平移,第一个到达的点(点的坐标为上面的 (xj,yj))则为最佳转移点(这时截距最小)。我们再考虑下什么样的点才能成为最佳转移点。
考虑三个决策点 i,j,k(i<j<k)。
当 ki,j>kj,k 时,如图:

显然,这时 j 不可能成为最佳转移点。
而当 ki,j<kj,k 时:
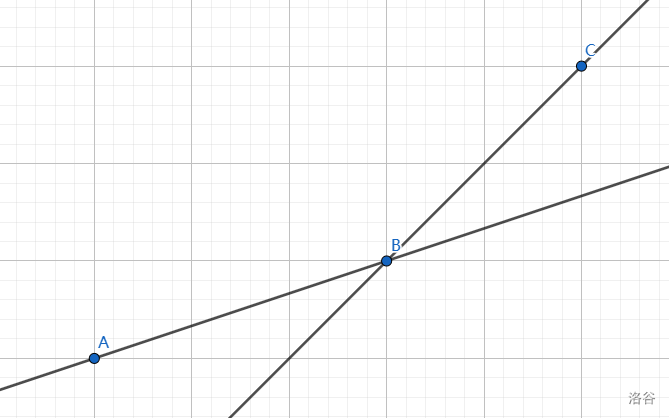
这时 j 可能成为最佳转移点。
因此,对于所有可能成为最佳转移点的点构成的点集,其斜率必然单调递增。这就是一个凸壳。我们只需要维护这个凸壳,然后查找第一个相交的点即可。(第一个相交的点 i 满足 ki−1,i<k≤ki,i+1)
现在问题变为了:如何维护这个凸壳?
这个问题很简单。只需要用一个单调队列,用类似找二维凸包的方式向外弹出斜率更大的队尾即可。
而题目中还有一个很好的条件:ti>0。因此 sumT 单调递增。我们在寻找相交的点时就可以不断从队头弹出无用决策(斜率小于当前的 k)。
这样就完成了,时间复杂度 O(n)。
加加强版
题意相同。
数据范围:n≤100000,−512≤ti≤512,0<ci≤512。
这时 ti 不满足单调递增的关系,我们无法每次从队头弹出元素,因为弹出的元素可能会成为以后的最佳转移点。因此我们需要维护整个凸包,在转移时,由于凸包上斜率单调递增,我们可以在单调队列里二分出第一个满足 ki−1,i<k≤ki,i+1 的凸包上的点,它就是最佳转移点。时间复杂度会多一个 logn。
加加加强版
ti,ci 都可能为负数。
这时横坐标和斜率都无法满足单调递增关系,这就意味着我们无法用单调队列动态维护凸包(可能会在中间插入)。这时常见的有三种解决方案:
- 平衡树
平衡树可以做到在数列中动态加入数,这时我们可以在平衡树上二分查找最佳转移点。十分好理解,但是难写。
- CDQ 分治
我们设 CDQ(l,r) 为计算 [l,r] 这段区间的 f 值。我们先递归计算 CDQ(l,mid)。这时假设我们已经计算完了左半边,考虑左半边对右半边的贡献。我们可以将 [l,mid] 的点组成的凸包建出来,因为这一部分已经计算完毕了,所以我们可以直接排序建凸包。
而对于右区间 [mid+1,r],我们也可以进行按斜率排序处理,这样就可以按照斜率单调递增的做法来弹出队头转移。最后再递归处理右区间 CDQ(mid+1,r)。
注意:处理右区间时不要将右区间的点加入凸包,因为我们计算的只是左区间对右区间的贡献,其余的贡献会继续递归处理。
- 李超线段树
我们可以再把转移方程搬过来:
f[i]−sumT[i]×sumC[i]−s×sumC[n]=j<imin{f[j]−(sumT[i]+s)×sumC[j])}
这时我们不按照上面的设法,我们重新理解下这个式子。
我们可以理解为有 i−1 条直线 1∼i−1,每条直线的斜率为 −sumC[j],截距为 f[j],而我们要查询当 x=sumT[i]+s 时的最值。这个可以直接用李超线段树维护。
习题
Cats Transport
有 m 只猫子,p 只铲屎官。有 n 座山,第 i 座山与第 i−1 座山的距离为 Di。这些猫子都去玩,猫子 i 去第 Hi 座山玩,在 Ti 时间结束游玩,然后在 Hi 傻等铲屎官来接它。铲屎官必须把所有猫子都带上,每个铲屎官以每秒 1 的速度不间断的从 H1 走到 Hn。每个铲屎官可以带上无限的猫子。现在安排每个铲屎官的出发时间(可以为负数),最小化猫子们的等待时间之和。求出最小等待时间之和。
数据范围:m≤100000,p≤100。
我们先设 Ai=Ti−∑i=2HiDi,即猫子能被接到的最早出发时间。因此如果铲屎官从 t 时刻出发,则这只猫子等待时间则为 t−Ai。
我们将 Ai 排序,设 s 为其排好序后的前缀和。利用临项交换法可以证明,一个铲屎官出发后带走的猫子在 A 中一定是连续的一段。这时我们就可以把问题转化为上面的任务安排。
我们考虑一只铲屎官带走 [l,r] 这些猫的代价为:
i=l∑r(Ar−Ai)=(r−l+1)Ar−sr+sl−1
我们设 f[i][j] 为前 i 只铲屎官带走了前 j 只猫子,则转移方程为:
f[i][j]=k<jmin{f[i−1][k]+(j−k)Aj−sj+sk}
这样复杂度为 O(m2p) 的,考虑斜率优化。
我们化简式子,能得到 f[i][j]+sj−j×Aj=mink<j{f[i−1][k]+sk−Aj×k}。这样就可以直接斜率优化了。
另外,本题可以加强数据到 p≤100000。这时我们可以用 wqs 二分来消去 i 这一维,使得时间复杂度降为 O(mlogp)。这里不再介绍。
Building Bridges
有 n 根柱子依次排列,每根柱子都有一个高度。第 i 根柱子的高度为 hi。
现在想要建造若干座桥,如果一座桥架在第 i 根柱子和第 j 根柱子之间,那么需要 (hi−hj)2 的代价。
在造桥前,所有用不到的柱子都会被拆除,因为他们会干扰造桥进程。第 i 根柱子被拆除的代价为 wi,注意 wi 不一定非负,因为可能政府希望拆除某些柱子。
现在政府想要知道,通过桥梁把第 1 根柱子和第 n 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。
数据范围:2≤n≤105;0≤hi,∣wi∣≤106。
本题很容易设出状态并写出转移方程:fi 表示 1∼i 建桥的代价,则
fi=j<imin{fj+(hi−hj)2+sumi−1−sumj}=j<imin{fj−sumj+hj2−2hi×hj}+sumi−1+hi2
这样就化为了斜率优化的形式,由于本题横坐标和斜率都不单调,则需要李超线段树或者 cdq 分治来优化。
The End




