NOIP2013-2023题解

本文章主要是为了不想卷题的时候不是特别颓废而准备

本文章是为了总结 NOIP 最近的题目（为了今年 NOIP 做准备），目前还没写完，尽量做的全面一些。

2013

积木大赛

给定一个长度为 $n$ 的序列 $h_i$，初始有一个全为 $0$ 的序列，每次操作可以任意选择 $L, R$，使得 $[L, R]$ 这段区间都加一，问最少操作多少次能使该序列与 $h$ 序列相同。

数据范围：$n \le 10^5$。

---

简单差分题，看到区间加就可以考虑差分。我们发现一次操作会使两个数一个加一一个减一，那么我们把 $h$ 差分以下，统计出来正数的和，就是答案。

转圈游戏

有 $n$ 个人（编号 $0\sim n-1$）围成一个环，一开始每个人都在自己编号相同的位置上，每轮过后每个人的位置都会变为 $(i+m)\bmod n$。一共进行了 $10^k$ 轮，问第 $x$ 个人走到了哪个位置。

数据范围：$k \le 10^9, n \le 10^6$。

---

裸题，每轮位置都会增加 $m$，则一共增加了 $m10^k$，则位置为 $(x+m10^k)\bmod n$。时间复杂度 $O(\log k)$。

花匠

给定一个序列 $h$，从其中选出一些数按顺序排列成序列 $g$，要求 $g$ 序列满足以下两种条件之一：

1. 对于所有在偶数的数 $g_i$，$g_{i-1}<g_i,g_i > g_{i+1}$，对于所有在奇数的数，$g_{i-1}>g_i,g_i < g_{i+1}$。
2. 对于所有在偶数的数 $g_i$，$g_{i-1}>g_i,g_i < g_{i+1}$，对于所有在奇数的数，$g_{i-1}<g_i,g_i > g_{i+1}$。

求满足条件的 $g$ 的最大长度。

数据范围：$n \le 10^5$。数据随机生成。

---

本题不难想到一个 $O(n^2)$ 的 dp，即设 $f_{i, 0/1}$ 为以第 $i$ 个位置结尾，且第 $i$ 个位置作为低点/高点时最多能放多少个数。我们可以写出状态方程：

$$\begin{aligned} f_{i,0}=\max _{j=1}^{i-1}\{f_{j,1}\}(h_i<h_j)\\ f_{i,1}=\max _{j=1}^{i-1}\{f_{j,0}\}(h_i>h_j) \end{aligned}$$

我们可以用树状数组或者线段树求一个前缀的最大值，但是本题有更简单的做法：

因为数据随机生成，我们可以运用人类智慧在转移的时候只取前 $500$ 个状态来转移。我们考虑如何卡掉这个做法，只需要构造一组有连续 $500$ 个数都上升的序列即可。但因为数据随机生成，这种概率极小，因此可以 AC。时间复杂度 $O(500n)$。

火柴排队

给定两个长度为 $n$ 的序列 $a, b$，规定这两个序列的距离为 $\sum (a_i-b_i)^2$。在序列中相邻的数都可以交换，求最少交换多少次可以使得这两个序列的距离最小。

数据范围：$n \le 10^5$。

---

易证距离最小的情况为 $a$ 序列中第 $k$ 大与 $b$ 序列的第 $k$ 大相对应，因此我们可以考虑如何做到这一点。显然，我们可以固定一个序列，只对另一个序列进行操作。我们只需要把第一个序列向第二个序列映射一下，求一下逆序对即可。我用的平衡树映射，常数巨大/kk。时间复杂度 $O(n\log n)$。

货车运输

有 $n$ 个城市，$m$ 条双向道路，每条道路有一个限重，货车只能通过限重大于等于它载货量的道路。现在有 $q$ 个货车，每条货车要从 $a_i$ 到 $b_i$ 送货，问每个货车最多能运送到多少货物。

数据范围：$n \le 10^4, m \le 5\times 10^4, q \le 3\times 10^4$。

---

贪心，我们可以求出最大生成树，然后直接在最大生成树上跑树剖或者倍增求最大值就行。时间复杂度 $O(n\log^2 n)$。

华容道

在一个 $n \times m$ 的棋盘上，只有一个位置是空白的，剩下的位置中有一部分是不可移动的旗子，一部分是可移动的旗子，还有一个是目标旗子。移动一次棋子需要一单位时间，且只能将棋子移动到空白位置，不能交换棋子的位置。给定 $q$ 次询问，问将目标旗子移动到给定的目标位置的最小时间。

数据范围：$n, m\le 30, q \le 500$。

---

搜索，不会，咕掉

2014

无线网络发射器选址

给定一个 $129 \times 129$ 的网格，有的点上有一些公共场合，现在要把一个无线网络发射器放到一个点上，该发射器能覆盖以它为中心边长为 $d$ 的正方形，问有多少种放置方案使得覆盖的公共场合最多，以及最多能覆盖多少公共场合。

数据范围：$d \le 20$。

---

裸题，二维前缀和即可。注意边界情况。

飞扬的小鸟

游戏界面是一个 $n \times m$ 的网格，其中有 $k$ 个管道，小鸟始终在游戏界面内移动，当小鸟飞到最右端时游戏完成。小鸟每一时刻向右移动一单位长度，同时玩家可以点击任意次屏幕，点击一次会使小鸟上升 $x_i$ 高度，如果不点击则会下降 $y_i$ 高度。小鸟高度为 $0$ 或者碰到管道时游戏结束。判断小鸟能否飞到最右端，如果可以，输出最小点击次数，如果不能，输出最多可以飞过多少管道。

数据范围：$n \le 10000, m \le 1000$。

---

我们设 $f_{i, j}$ 为当小鸟在 $x=i, y=j$ 时所需的最小点击次数。不难得到转移方程 $f[i][j]=\max _{k=0}\{ f[i - 1][j+y_{i-1}], f[i-1][j+kx_{i-1}]\}$。这时我们先暂时不考虑下降的转移，我们就可以发现这其实是一个完全背包。因此我们就可以把这个 $O(n^3)$ 的转移方程用完全背包的方法变为 $O(n^2)$。当遇到管道时判一下是否无解即可。

寻找道路

给定一张边权全为 $1$ 的有向图，要求找到一条最短路满足路径上所有点的出边指向的点都直接或间接与终点相通。如果不存在，输出 $-1$。

数据范围：$n \le 10000, m \le 200000$。

---

先建反图，从终点开始 bfs，找到终点走不到的点就是无法走的点。再用这些无法走的点更新它周围一圈的点，让这些点也不能走。最后跑一遍 bfs 求最短路即可。时间复杂度 $O(n + m)$。

联合权值

给定一棵树，每个点有权值 $w_i$，对于有序点对 $(u, v)$，当 $dist_{u, v}=2$ 时，它们会产生 $w_u \times w_v$ 的权值。问所有有序点对中权值最大是多少，以及这些权值之和。

数据范围：$n \le 200000$。

---

设 $f[i][j]$ 为在以 $i$ 为根的子树中距离它 $j$ 的点的权值和，$g[i][j]$ 同理，为最大值。树形 dp 求出所有的 $f[i][2], g[i][2]$，在树形 dp 的同时计算一下子树内经过 lca 的点对权值。最后再计算一段为 lca 的权值，即为 $w_i \times f[i][2]$。因为题目要求是有序点对，乘二即可。时间复杂度 $O(n)$。

解方程

给定方程 $a_0+a_1x+a_2x^2+\cdots +a_nx^n=0$，求出这个方程在 $[1,m]$ 范围内的整数解。

数据范围：$n \le 100, |a_i|\le 10^{10000},m \le 10^6$。

---

最无语的一道题…

直接暴力枚举，对于大范围的 $a_i$，我们的应对方法是搞一个模数，将所有运算取模，在模意义下如果结果为 $0$ 则该数大概率是方程的解。如果不放心可以取两个模数。计算左边的多项式可以直接秦九韶算法，复杂度 $O(nm)$。

2015

神奇的幻方

给定构造方法，要求构造一个幻方。

首先将 $1$ 写在第一行的中间。

之后，按如下方式从小到大依次填写每个数 $K (K=2,3,\cdots,N \times N)$ ：

1. 若 $(K-1)$ 在第一行但不在最后一列，则将 $K$ 填在最后一行， $(K-1)$ 所在列的右一列；
2. 若 $(K-1)$ 在最后一列但不在第一行，则将 $K$ 填在第一列， $(K-1)$ 所在行的上一行；
3. 若 $(K-1)$ 在第一行最后一列，则将 $K$ 填在 $(K-1)$ 的正下方；
4. 若 $(K-1)$ 既不在第一行，也不在最后一列，如果 $(K-1)$ 的右上方还未填数，则将 $K$ 填在 $(K-1)$ 的右上方，否则将 $K$ 填在 $(K-1)$ 的正下方。

数据范围：$n \le 39$ 且 $n$ 为奇数。

---

按题意构造即可，简单题。

信息传递

有 $n$ 个人，每个人有一个传递对象，每轮每个人都会把自己上一轮获得的信息传递给他（一开始每个人都有自己的信息），问多少轮之后有人会得到自己一开始的信息。

数据范围：$n \le 2\times 10^5$。

---

建出来图，就是一个裸的拓扑找环问题，找到之后直接记录大小即可。

时间复杂度 $O(n)$。

跳石头

有 $n$ 个石头（不包括起点和终点的石头），现在准备移走这 $n$ 个石头中的 $m$ 个，问移走这些石头后剩余石头（包括起点）最短间距的最大值。

数据范围：$n, m \le 50000$。

---

简单二分，二分最大值，然后按照题意模拟移走石头即可。时间复杂度 $O(n\log n)$。

子串

有两个字符串 $A$ 和 $B$，现在要从 $A$ 字符串中选出 $k$ 个不重叠的非空子串，然后把这些子串按照在 $A$ 中出现的顺序拼接起来形成一个新字符串，有多少种方案能使得新字符串和 $B$ 字符串相同。

数据范围：$|A| \le 1000, |B| \le 200, k \le 200$。

---

有意思的 dp 题。我们设 $f[i][j][k][0/1]$ 为当前用到了 $A$ 的前 $i$ 个字符，$B$ 的前 $j$ 个字符，目前 $A$ 串选了 $k$ 个子串，$A$ 中第 $i$ 位是否被选上的方案数。

显然就有以下转移方程：

$$\begin{aligned} f[i][j][k][0]&=f[i-1][j][k][0]+f[i-1][j][k][1]\\ f[i][j][k][1]&=f[i-1][j-1][k-1][0]+f[i-1][j-1][k][1]+f[i-1][j-1][k-1][1](A_i=B_i) \end{aligned}$$

第一个式子表示当前这一位不用来匹配，则枚举前一位是否用来匹配。第二个式子表示当前如果相等，那么枚举：上一位不匹配、这一位和上一位一起放到一个串、这一位另开一个串。这样就完成了转移。

再考虑边界情况。显然，当 $A_i=B_1$ 时，$f[i][1][1][1]=1$。而 $f[i][1][1][0]$ 就等于 $1\sim i-1$ 这些位中满足 $A_i=B_i$ 的数量。

这样就做完了。时间复杂度 $O(nmk)$。

斗地主

给定斗地主的出牌规则，问当前的手牌至少打多少次才能打完。

数据范围：$T \le 100, n\le 23$。

---

搜索题，必然不写。

运输计划

有 $n$ 个星球和 $n-1$ 条道路。第 $i$ 条道路经过的时间为 $t_i$，现在同时有 $m$ 个运输计划，每个计划要从 $u$ 到 $v$，任意两条飞船间不会干扰。现在可以把一条航道经过的时间改为 $0$，最终所有运输计划完成的最短时间是多少。

数据范围：$n,m\le 3\times 10^5$。

---

本题可以转化问法：让所有运输计划完成的时间的最大值最小。这样就是一个比较明显的二分了。我们二分最短时间，然后考虑如何判定。

首先时间小于 $mid$ 的线路可以直接不管，这些线路不管改不改都可以满足条件。而大于 $mid$ 的线路我们需要找出它所覆盖的路径，这个可以直接用树上差分解决。找到所有路径的覆盖次数后我们检查是否有路径被所有大于 $mid$ 的线路覆盖了，如果没有则直接退出。因为不管怎么覆盖，总会有大于 $mid$ 的线路不会减少时间。而如果满足上一个要求，我们再考虑去掉一条被所有路径覆盖的边。再检查去掉边后能不能让最长的线路时间小于 $mid$，这样就完成了。

时间复杂度 $O(n\log n)$。

2016

玩具谜题

有 $n$ 个小人，有的面朝内有的面朝外，现在有 $m$ 条命令，每条命令形如左数/右数 $x$ 个人，问执行完这些命令后到达的是哪个小人。

数据范围：$n\le 10^5$。

---

模拟题，过。

组合数问题

给定固定的 $k$，再给定 $n, m$，求对于所有 $0\le i \le n, 0\le j \le \min(i,m)$ 有多少对 $(i, j)$ 满足 $k|\dbinom{i}{j}$。

数据范围：$n, m\le 2000, T\le 10^4$。

---

询问次数巨大，考虑预处理。我们设 $f_{n, m}$ 为 $1 \le i\le n, 1\le j\le m$ 的情况下有多少满足条件的 $(i,j)$。这个直接用前缀和来统计即可，$f_{n,m}=f_{n-1,m}+f_{n,m-1}-f_{n-1,m-1}+[k|\dbinom{n}{m}]$。

时间复杂度 $O(n^2)$。

换教室

有 $n$ 节课程，$v$ 个教室，$e$ 条道路，每节课程原先是在第 $c_i$ 个教室上课，可以申请换到第 $d_i$ 个教室上课。每节课结束后都会从当前教室选择耗费体力最少的道路到下一个教室上课。

现在有 $m$ 次申请换教室的机会（可以不用完），对于第 $i$ 节课程，申请通过的概率为 $p_i$，每节课程只能申请一次。问怎么申请才能让他移动消耗的体力值的期望最小，求出最小值。

数据范围：$n,m\le 2000, v\le 300, e\le 90000$。

---

我们先跑一遍 floyd，求出两点之间的最短路，方便后面的 dp。

我们设 $f[i][j][0/1]$ 为当前考虑到第 $i$ 节课程，用了 $j$ 次申请机会，当前这节课程是否申请的期望。分析一下就能得出以下转移方程：

$$\begin{aligned} f[i][j][0] &= \min(f[i][j][0], f[i - 1][j][0] + dist[c[i - 1]][c[i]]);\\ f[i][j][0] &= \min(f[i][j][0], f[i - 1][j][1] + dist[d[i - 1]][c[i]] * p[i - 1] + dist[c[i - 1]][c[i]] * (1 - p[i - 1])); \end{aligned}$$

当前申请的转移方程也同理可以推出，这里就不再写出~~（放不下了）~~。

时间复杂度 $O(n^3+nm)$。

蚯蚓

有 $n$ 只蚯蚓，每秒会选择长度最长的蚯蚓（长度记为 $x$），将其切成长度为 $\left \lfloor px \right \rfloor$ 和 $x-\left \lfloor px \right \rfloor$ 两只蚯蚓。除了这新产生的两只蚯蚓之外，剩下的蚯蚓都会增加 $q$ 的长度。

求出 $m$ 秒内每秒被切断的蚯蚓的长度，以及 $m$ 秒后所有蚯蚓的长度。

数据范围：$n\le 10^5, m\le 7\times 10^6$。

---

我们先考虑 $O(n\log n)$ 的做法。我们维护一个大根堆，每次取出队头并将其切成两半再放回去，同时我们可以维护这个堆整体的偏移量 $\delta$。每次要插入 $x$ 时实际插入的为 $x-\delta$，取出也同理。这样就求出了所有时间内的答案。

但是这样时间复杂度不够优秀，考虑如何将 $\log$ 干掉。我们要发现一个潜在的单调性，就是我们先切成两半的蚯蚓的第一部分一定大于后切成两半的蚯蚓的第一部分，第二部分也同理。这里证明略过，可以感性理解，具体证明需要用到下取整的一些性质。

于是我们可以维护三个队列，一个放排过序的原先的蚯蚓，一个放切出来第一部分的蚯蚓，一个放切出来第二部分的蚯蚓，同时维护一个整体偏移量。每次从三个队头中取最大的切开即可。这样时间复杂度就可以达到 $O(n)$。

愤怒的小鸟

平面直角坐标系中有 $n$ 只小猪，坐标分别为 $(a_i,b_i)$。现在要从坐标原点发射小鸟攻击小猪，每个小鸟的运动轨迹为 $y=ax^2+bx$ 的抛物线，所有在这条抛物线上的小猪都会被消灭。问至少发射多少小鸟才能把所有小猪消灭。

数据范围：$n\le 18$。

---

我们可以找出所有经过至少 $2$ 只小猪的抛物线，将其解析式求出并求出它经过哪些小猪。然后用最少的抛物线覆盖所有小猪，这是一个经典的重复覆盖问题，可以用 DLX 来求解。但是这样过于复杂，我们考虑用状压的方法。我们可以将一条抛物线状压成一个整数，用或运算来表示覆盖，这里不再详细说明。

时间复杂度 $O(2^n)$。

天天爱跑步

游戏的地图是一颗有 $n$ 个节点的树，现在有 $m$ 个玩家，每个玩家起点为 $s_i$，终点为 $t_i$，以每秒一条边的速度前进。每个节点上都有一个观察员，在节点 $j$ 的观察员会在第 $w_j$ 秒观察到当前到这个节点的人。求每个节点的观察员能够观察到多少人。

数据范围：$n, m\le 3\times 10^5$。

---

我们把一条路径拆分成两类：从 $s$ 到 $lca$ 和从 $lca$ 到 $t$。我们只考虑前一段，后一段也是同理的。

我们把一个人能被观察到的式子写出来：$w_u=dep_u-dep_s$。我们移一下项可以得到：$w_u-dep_u=dep_s$。这就相当于给这条路径上所有点发放一个 $dep_s$ 类型的物品，最终查询的是 $w_u-dep_u$ 种物品的数量。这个可以用线段树合并+树上差分来解决。

向下的路径同理，注意相减可能会出现负数，我们需要将值域整体平移。

时间复杂度 $O(n\log n)$。

2017

小凯的疑惑

给定两种硬币，硬币面值互质，每种硬币都有无限个。问最小的不能拼凑出来的面额是多少。

数据范围：没有

---

答案为 $ab-a-b$。证明如下：

考虑当两个硬币都至少选一个时，因为 $a,b$ 互质，最小不能表示的数是 $ab$。而每个硬币可以不选，因此答案为 $ab-a-b$。

奶酪

有一块高度为 $h$ 的三维奶酪，其中有 $n$ 个半径为 $R$ 的球形空隙。当球相切或相交时可以钻过去。问从底面是否能钻到顶。

数据范围：$n\le 10^3$。

---

$i$ 空心和 $j$ 空心连通的条件为 $dist_{i, j} \le 2R$。我们可以两两枚举，然后用并查集维护连通性即可。

时间复杂度 $O(n^2)$。

时间复杂度

小明正在学习一种新的编程语言 A++，刚学会循环语句的他激动地写了好多程序并 给出了他自己算出的时间复杂度，可他的编程老师实在不想一个一个检查小明的程序， 于是你的机会来啦！下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。

A++语言的循环结构如下：

F i x y
    循环体
E

其中F i x y表示新建变量 $i$（变量 $i$ 不可与未被销毁的变量重名）并初始化为 $x$， 然后判断 $i$ 和 $y$ 的大小关系，若 $i$ 小于等于 $y$ 则进入循环，否则不进入。每次循环结束后 $i$ 都会被修改成 $i+1$，一旦 $i$ 大于 $y$ 终止循环。

$x$ 和 $y$ 可以是正整数（$x$ 和 $y$ 的大小关系不定）或变量 $n$。$n$ 是一个表示数据规模的变量，在时间复杂度计算中需保留该变量而不能将其视为常数，该数远大于 $100$。

E 表示循环体结束。循环体结束时，这个循环体新建的变量也被销毁。

数据范围 $T \le 100$。

---

中模拟。开一个栈来维护循环和跳出循环，用哈希表存储变量，记得多测清空即可。

逛公园

有一张 $n$ 个点，$m$ 条边的无向图，边有边权。从 $1$ 号点到 $n$ 号点的最短路记为 $d$，求有多少 $1$ 到 $n$ 的路径满足长度小于等于 $d+K$。

数据范围：$n\le 10^5, m\le 2\times 10^5, K \le 50$。

---

先求出最短路，再考虑 dp。我们设 $f[i][j]$ 为 $1$ 号点到 $i$ 号点，路径长度比 $dist[i]$ 长 $j$ 的路径个数。考虑如何转移。

我们先对 $(u,v,w)$ 这条边考虑，列出下面这些式子：

$$dist[v] = dist[u]+w$$

$$d_{f[v][x]} = dist[v]+x$$

$$d_{f[u][k]}=dist[u]+k$$

根据这三个式子联立，我们就可以得出 $f[u][k]$ 能够更新的状态 $f[v][x]$（$x=dist[v]+k - w-dist[u]$）。跑一下记忆化搜索即可。至于无解的情况，判一下是否存在 $0$ 环即可。

时间复杂度 $O(n\log n+nk)$。

宝藏

有 $n$ 个宝藏屋和 $m$ 条道路。现在可以免费打通一条地面到宝藏屋的道路。接下来要开凿宝藏屋之间的道路，新开发一条道路的代价为 $K\times L$，$K$ 为从地面到该宝藏屋的所经过的宝藏屋的数量，$L$ 表示这条道路的长度，两个已经被发掘的宝藏屋之间的道路无需再开发。要求最终所有宝藏屋都被开发，求最小代价。

数据范围：$n\le 12, m\le 1000$。

---

注意到本题数据范围很小，我们可以考虑状压或暴搜。我们设 $f[i][S]$ 为当前打通的宝藏屋的最大深度为 $i$，已经打通的宝藏屋的状态为 $S$。我们考虑如何转移。我们可以枚举 $S$ 的子集 $T$，表示深度为 $i-1$ 的时候打通的宝藏屋，再用 $f[i-1][T]$ 来更新 $f[i][S]$。时间复杂度 $O(n3^n)$。

列队

有一个 $n\times m$ 的方阵。初始时，第 $i$ 行 $j$ 列的学生编号为 $(i-1)\times m+j$。队伍中可能有人要离队，每一个离队时间可以用 $(x, y)$ 描述，表示第 $x$ 行 $y$ 列的学生离开。

有学生离队后，教官会依次下达两条命令：

1. 向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条 指令之后，空位在第 $x$ 行第 $m$ 列。
2. 向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条 指令之后，空位在第 $n$ 行第 $y$ 列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 $n$ 行 第 $m$ 列一个空位，这时这个学生会自然地填补到这个位置。

求出每次离队同学的编号。

数据范围：$n,m,q\le 3\times 10^5$。

---

本题比较容易想到可以用平衡树来维护每一行的信息，但是本题主要的问题是在于空间。我们可以注意到，每次有人离开改变的只是一大整块的位置。因此我们可以考虑类似珂朵莉树的思想，把一段区间压缩成一个节点，当要改变信息的时候我们可以从一段区间内分裂出来一段区间。这样就可以满足空间的限制了。

剩下的就是 fhq 的板子了，平衡树分裂、合并。

分裂出区间的代码：

inline void split(int p, int k)
{
    if(k >= t[p].R - t[p].L + 1) return;
    int w = t[p].L + k - 1;
    int q = New(w + 1, t[p].R);
    t[p].R = w;
    t[p].r = merge(q, t[p].r);
    pushup(p);
}

时间复杂度 $O(n\log n)$。

2018

铺设道路

有一条有 $n$ 块区域的道路，第 $i$ 块区域的下降深度是 $d_i$，每天可以使一段区间的下降深度减一。至少多少天能使所有的下降深度为 $0$。

数据范围：$n\le 10^5$。

---

差分，简单题。

货币系统

有 $n$ 种不同的货币，每种货币的面额为 $a[i]$，我们将这个货币系统记为 $(n,a)$。定义两个货币系统 $(n,a)$ 和 $(m,b)$ 等价为：对于任意非负整数 $x$，它要么能被两个货币系统同时表出，要么不能被其中任意一个表出。现在给定一个货币系统 $(n,a)$，求与之等价的 $(m,b)$ 且 $m$ 尽可能小。

数据范围：$n\le 100, a[i]\le 25000$。

---

本题重点在证明上，先给出本题需要的结论：$B\subseteq A$。

我们先考虑证明一个结论：任何在 $A$ 中只有自己能表示自己的数字一定会出现在 $B$ 中。

设 $x\in A$ 并且 $x$ 不能被 $A$ 中其他数字表示。假设 $x\not \in B$，那么 $B$ 中一定有一些元素能够组成 $x$。因为如果所有元素都存在于 $A$ 的话，$x$ 就能被 $A$ 中其他数字表示，所以这些元素中至少有一个不存在于 $A$ 中且不能被 $A$ 中其他元素表示的数字，与定义不符。

因此任何在 $A$ 中只有自己能表示自己的数字一定会出现在 $B$ 中。

有了这个结论后再去证明 $B\subseteq A$。

我们设 $x\in B$ 且 $x\not \in A$。那么 $x$ 一定能被 $A$ 中一些只有自己能表示自己的数字组成，根据上面的结论，这些数字都会存在于 $B$ 中，那么这些数字就能表示出来 $x$，与题目要求的最小 $m$ 不符。因此 $B\subseteq A$。

证明完结论后，题目就好做了。我们先把 $a$ 排个序，设 $f_{j}$ 为能否拼成 $j$。转移就是 $f_j=f_j|f_{j-a[i]}$。

时间复杂度 $O(na)$。

赛道修建

有 $n$ 个路口，$n-1$ 条道路，每条道路都有长度 $w_i$，现在要修建 $m$ 条赛道。每条赛道包含一条树上的路径，且每条道路只能被一条赛道经过。一条赛道的长度为包含所有道路的长度和。求出长度最小的赛道长度的最大值。

数据范围：$n \le 5\times 10^4$。

---

这种最小值最大的问法大部分都是二分。现在的关键就是 check 函数怎么写。

我们考虑在树上的一个节点，它的儿子有 4 种情况可以选择：和另一个儿子形成赛道、和父亲及以上路径形成赛道、不形成赛道、和当前到父亲这条边形成赛道。我们可以在每个节点记录一个向上传递的值，为这四种情况做准备。

第四种情况无疑是最优的，要直接选上。剩下的儿子我们两两配对，根据贪心的思想，要选择一个稍微小一些的儿子和它形成赛道，我们就可以用一个 set 查询后继。如果没有后继，就把它变为向上传递的值给父亲。最后判断是否选够 $m$ 条赛道。这样就可以完成统计。

时间复杂度 $O(n\log^2n)$。

旅行

有 $n$ 个城市和 $m$ 条双向道路，$n$ 个城市连通。每条道路只能走两次：走过去和回退回来。每到一个新城市则会记录下它的编号，最终形成一个长度为 $n$ 的序列 $A$。当回到起点时，如果所有城市都被访问到，则结束旅行。求字典序最小的序列 $A$。

数据范围：$n\le 5000$，$m=n-1$ 或 $m=n$。

---

本题数据范围决定了这是一道树相关题目。我们先考虑 $m=n-1$ 的情况，这时明显是一棵树，我们只需要贪心地选择字典序最小的儿子节点走即可。

而 $m=n$ 的情况就是一颗基环树了。我们发现，最终走过的路径中一定有一条边没有访问到，我们就可以枚举环上的边，同时断边跑树的情况。最后字典序比较即可。时间复杂度 $O(n^2\log n)$。

填数游戏

有一个 $n\times m$ 的矩形网格，玩家需要在每个表格中填入 $0$ 或 $1$。填数的时候需要满足一些限制：

定义合法路径 $P$ 为：从矩阵的左上角 $(0,0)$ 出发，走到矩阵的右下角 $(n-1,m-1)$，且每次只能移动到和它相邻且在它右边或下边的格子。

对于一条路径，我们可以把它用一个长度为 $n+m-2$ 的字符串表示 $w(P)$，其中只包含 $R$ 和 $D$。同时将路径上经过的所有格子上的数字连接起来会形成一个长度为 $n+m-1$ 的 $01$ 串 $s(P)$。游戏要求找到一种填数字的方法，使得对于两条路径 $P_1, P_2$，如果 $w(P_1)>w(P_2)$，那么 $s(P_1)\le s(P_2)$。求有多少种满足条件的合法方案。

数据范围：$n\le 8, m\le 10^6$。

---

打表找规律题，不会。

保卫王国

有 $n$ 个城市，$n-1$ 条道路，现在要驻扎军队，要求每条边的两个端点中至少要有一个城市驻扎军队。在第 $i$ 个城市驻扎军队要花费 $p_i$ 元。

现在有 $q$ 次询问，每次询问规定两个城市是否驻扎军队，然后回答当前驻扎军队花费的最小值。询问和询问之间相互独立。

数据范围：$n, q\le 10^5$。

---

本题有动态 dp 的做法，但是不在讨论范围内。

我们先考虑如果没有强制选择的要求，这题就是一个比较简单的树形 dp，设 $f[i][0/1]$ 为 $i$ 子树中这个点选择/不选择驻扎军队的最小花费，转移为：

$$\begin{aligned} f[u][0]&=\max _{v\in \mathrm{son}_u }(f[v][1])\\ f[u][1]&=\max _{v\in \mathrm{son}_u }(f[v][0], f[v][1])+p[u] \end{aligned}$$

我们可以发现，如果强制规定的两个点 $u$ 和 $v$ 的状态，那么受影响的转移只有 $u$ 到 $lca$，$v$ 到 $lca$，以及 $lca$ 到根的路径上的点。我们就可以用树上倍增来维护这个东西。

我们设 $fh[i][j][0/1][0/1]$ 为 $i$ 的第 $2^j$ 祖先（以下称为 $anc$）的子树中除去 $i$ 的子树，且 $i$ 的状态为 $0/1$，$anc$ 的状态为 $0/1$ 时的最小花费。这个可以很简单的用倍增求出。之后我们在将 $u\to lca$ 和 $v\to lca$ 这两条路径倍增转移时，我们枚举祖先的状态然后进行转移。

同时，因为将 $u$ 和 $v$ 转移到 $lca$ 之后还要继续向上转移，同时还要加上其他树的贡献，我们再设 $g[i][0/1]$ 为整棵树除去 $i$ 的子树，且 $i$ 的状态为 $0/1$ 的最小花费。这个数组可以直接 dp 求出。

最后倍增到 $lca$ 的儿子之后，我们再枚举 $lca$ 选或不选，同时加上除去 $lca$ 其他子树的贡献，即为答案。

时间复杂度 $O(n\log n+q\log n)$。

倍增部分代码：

inline int solve(int x, int a, int y, int b)
{
    if(dep[x] < dep[y]) swap(x, y), swap(a, b);
    int tx[2] = {INF, INF}, ty[2] = {INF, INF};
    int nx[2], ny[2];
    tx[a] = f[x][a], ty[b] = f[y][b];
    for(int i = 18; i >= 0; i -- )
    {
        if(dep[fa[x][i]] >= dep[y])
        {
            nx[0] = nx[1] = INF;
            for(int u = 0; u < 2; u ++ )
                for(int v = 0; v < 2; v ++ )
                    nx[u] = min(nx[u], tx[v] + fh[x][i][v][u]);
            tx[0] = nx[0], tx[1] = nx[1];
            x = fa[x][i];
        }
    }
    
    if(x == y) return tx[b] + g[x][b];

    for(int i = 18; i >= 0; i -- )
    {
        if(fa[x][i] != fa[y][i])
        {
            nx[0] = nx[1] = ny[0] = ny[1] = INF;
            for(int u = 0; u < 2; u ++ )
                for(int v = 0; v < 2; v ++ )
                {
                    nx[u] = min(nx[u], tx[v] + fh[x][i][v][u]);
                    ny[u] = min(ny[u], ty[v] + fh[y][i][v][u]);
                }
            tx[0] = nx[0], tx[1] = nx[1];
            ty[0] = ny[0], ty[1] = ny[1];
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    int lca = fa[x][0];
    int ans0 = f[lca][0] - f[x][1] - f[y][1] + tx[1] + ty[1] + g[lca][0];
    int ans1 = f[lca][1] - min(f[x][1], f[x][0]) - min(f[y][0], f[y][1]) + min(tx[0], tx[1])
                + min(ty[0], ty[1]) + g[lca][1];
    return min(ans0, ans1);
}

upd on 2023.8.28：

动态 dp 的做法应该也不难，也只是按照普通的转移方程搞就完了，然后套个矩阵再放树上跑就完事了。

2020

排水系统

有 $n$ 个排水节点和 $m$ 个单向排水管道。排水系统中还有一些是污水接受口，这些接受口没有污水进入的管道。同时还有一些是排水口，这些排水口没有向外的排水管道。现在每个污水接受口都有一吨污水，污水进入每个节点后，会均等地从每个排出管道流向其他节点。排水管道不会出现环。

问最终每个排水口都会有多少污水。

数据范围：$n\le 10^5$。

---

拓扑排序板子题，跑拓扑的时候记录一下就行。分数的问题可以直接写一个结构体，注意 __int128。

字符串匹配

定义 $A^1=A$，$A^n = A^{n - 1} A$（$n \ge 2$ 且为正整数）。求 $S = {(AB)}^iC$ 的方案数，其中 $F(A) \le F(C)$，$F(S)$ 表示字符串 $S$ 中出现奇数次的字符的数量。两种方案不同当且仅当拆分出的 $A$、$B$、$C$ 中有至少一个字符串不同。

数据范围：$|S|\le 10^6$。

---

我们先不考虑 $F(A) \le F(C)$ 的限制。我们现在先枚举循环的长度，我们现在要找出有多少循环（这时我们先把 $A$ 和 $B$ 看作整体）。我们考虑用 exkmp 来求。

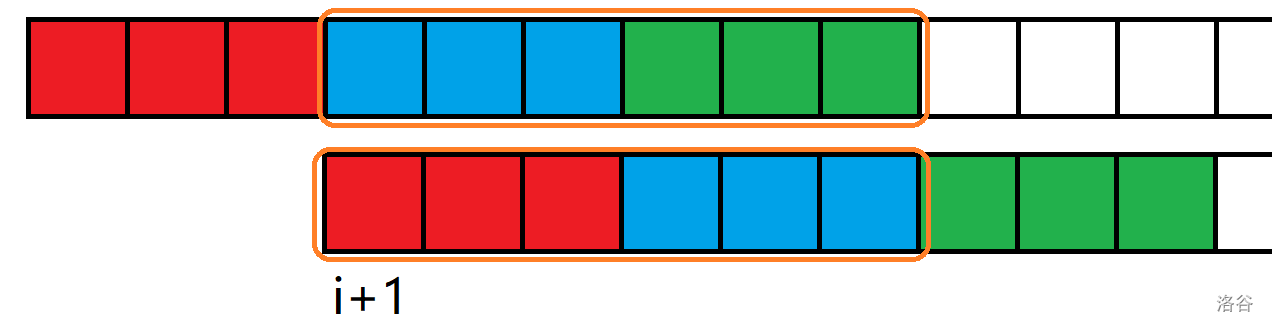
我们先把原字符串和原字符串的第 $i + 1$ 位对齐。见下图：

我们可以清楚的看到相同颜色部分是相同的，框起来的部分也是相同的。手玩下就能得到当循环长度为 $i$ 时循环的个数为 $\left \lfloor \frac{z[i+1]}{i} \right \rfloor +1$。

现在我们加上 $F$ 的限制，我们考虑分情况讨论。我们将前缀分为由奇数个循环拼成和偶数个循环拼成。假设一共有 $t$ 个循环，那么显然由奇数个循环拼成的前缀有 $t - \left \lfloor \frac{t}{2} \right \rfloor$，偶数个的前缀有 $\left \lfloor \frac{t}{2} \right \rfloor$ 个。我们下面来分类讨论。

当有奇数个循环时，我们考虑剩下的后缀的字母奇偶性都是等价的。因为我们加入两个循环时字符的奇偶性必然不会改变。因此我们维护单个变量 $suf_i$ 维护 $s[i\sim n]$ 的奇数字符的个数，同时维护 $pre_i$ 为 $s[1\sim i]$ 的奇数字符的个数。我们找符合要求的奇数循环个数时我们只需要寻找有多少前缀 $j$ 满足 $pre_j\le suf_i$（$i$ 为枚举的循环长度）

而对于偶数个循环时同理，只不过 $C$ 的字母奇偶性和整个字符串相同。因此我们依旧维护 $pre_i$，我们只要寻找有多少前缀 $j$ 满足 $pre_j\le all$ 即可。而对于前缀查询，直接树状数组即可。

时间复杂度 $O(n\log 26)$。

移球游戏

有 $n + 1$ 根柱子，柱子从 $1 \sim n + 1$ 编号，其中 $1$ 号柱子、$2$ 号柱子、……、$n$ 号柱子上各有 $m$ 个球，它们自底向上放置在柱子上，$n + 1$ 号柱子上初始时没有球。这 $n \times m$ 个球共有 $n$ 种颜色，每种颜色的球各 $m$ 个。

初始时一根柱子上的球可能是五颜六色的，任务是将所有同种颜色的球移到同一根柱子上，这是唯一的目标，而每种颜色的球最后放置在哪根柱子则没有限制。

可以通过若干次操作完成这个目标，一次操作能将一个球从一根柱子移到另一根柱子上。更具体地，将 $x$ 号柱子上的球移动到 $y$ 号柱子上的要求为：

1. $x$ 号柱子上至少有一个球；
2. $y$ 号柱子上至多有 $m - 1$ 个球；
3. 只能将 $x$ 号柱子最上方的球移到 $y$ 号柱子的最上方。

使用的操作次数不能超过 $820000$。

---

恶心构造题。

我们先把我们当前要移动的颜色设为 $1$，其他颜色设为 $0$，我们的目标就变成了构造一个全 $1$ 列。

为了构造全 $1$ 列，我们先构造一个全 $0$ 列。具体的构造方法是：

• 先设第一列的 $1$ 的个数为 $x$，设空列为第 $n+1$ 列。
• 把第 $n$ 列最上面 $x$ 个球移动到第 $n+1$ 列
• 然后把第一列的球分开，$1$ 放到第 $n$ 列最上面，$0$ 放到第 $n+1$ 列。
• 把第 $n+1$ 列的 $m-x$ 个 $0$ 移动到第一列
• 把第二列的 $0$ 全部移动到第一列，塞不下的话就放到第 $n+1$ 列。

这样我们就使得第一列全为 $0$。这样能成功的原因就是前两列中 $0$ 的个数肯定大于等于 $m$，我们这样做的本质其实就是用 $1, 2, n, n+1$ 这些列来构造全 $0$ 列。

接下来就是用全 $0$ 列来构造全 $1$ 列了。

• 我们先设空列为第 $n+1$ 列，全 $0$ 列为第 $n$ 列。
• 我们按照上面相同的方法把第一列的 $1$ 放到第 $n$ 列，$0$ 放到第 $n+1$ 列。
• 这时我们手玩可以发现，第 $n+1$ 列变为了新的全 $0$ 列，第 $n$ 列变为了只有最上面是 $1$ 的一列，而第 $1$ 列变成了空列。

这样不断做就能把所有 $1$ 放到最上面。然后移动到空列即可。

但是我们发现当 $n=2$ 时，第二列和第 $n$ 列是相同的，因此需要特判。

• 设空列为第 $3$ 列。
• 我们先把第一列的 $1$ 分解到第 $2$ 列，$0$ 分解到第 $3$ 列。
• 然后再把第一列放出来的重新放回第一列（先 $1$ 后 $0$），这样就给第一列排了个序。
• 我们再把第三列剩下的都重新放回第二列，再把第一列的 $0$ 都放到第三列。
• 最后把第二列分解到第一列和第三列即可。

最终总操作次数：

构造全 $0$ 列需要 $4m$ 次，构造全 $1$ 列需要 $nm+m$ 次，因此总操作次数为 $\sum \limits_{i=1}^n im+5m=60000$ 次左右。

微信步数

小 C 喜欢跑步，并且非常喜欢在微信步数排行榜上刷榜，为此他制定了一个刷微信步数的计划。

他来到了一处空旷的场地，处于该场地中的人可以用 $k$ 维整数坐标 $(a_1, a_2, \ldots , a_k)$ 来表示其位置。场地有大小限制，第 $i$ 维的大小为 $w_i$，因此处于场地中的人其坐标应满足 $1 \le a_i \le w_i$（$1 \le i \le k$）。

小 C 打算在接下来的 $P = w_1 \times w_2 \times \cdots \times w_k$ 天中，每天从场地中一个新的位置出发，开始他的刷步数计划（换句话说，他将会从场地中每个位置都出发一次进行计划）。

他的计划非常简单，每天按照事先规定好的路线行进，每天的路线由 $n$ 步移动构成，每一步可以用 $c_i$ 与 $d_i$ 表示：若他当前位于 $(a_1, a_2, \ldots , a_{c_i}, \ldots, a_k)$，则这一步他将会走到 $(a_1, a_2, \ldots , a_{c_i} + d_i, \ldots , a_k)$，其中 $1 \le c_i \le k$，$d_i \in \{-1, 1\}$。小 C 将会不断重复这个路线，直到他走出了场地的范围才结束一天的计划。（即走完第 $n$ 步后，若小 C 还在场内，他将回到第 $1$ 步从头再走一遍）。

小 C 对自己的速度非常有自信，所以他并不在意具体耗费的时间，他只想知道 $P$ 天之后，他一共刷出了多少步微信步数。请你帮他算一算。

数据范围：$1 \le n \le 5 \times {10}^5$，$1 \le k \le 10$，$1 \le w_i \le {10}^9$，$d_i \in \{-1, 1\}$。

---

T4 逆天题。

我们可以把答案转化一下，这些天的步数之和可以转化为对于每天，没有走出边界的点的数量之和。由于每一维互相独立，假设第 $j$ 维第 $i$ 天存活的点的范围是 $[l_{j, i}, r_{j, i}]$，那么这一天的贡献就是 $\prod _{j=1}^{k}(r_{j, i}-l_{j, i}+1)$。

我们可以暴力模拟每一维，同时计算这个贡献。但是面对题目的数据范围无法通过，我们考虑优化。

为了方便，我们下面说的都是考虑第 $j$ 维的情况。

设 $[l_i, r_i]$ 为第一轮中第 $i$ 步时历史最大位移，那么这时死掉的点有 $r_i-l_i$ 个。我们假设一轮走完后的偏移量为 $e_j$，那么第二轮第 $i$ 步时的最大偏移量为 $[\min(l_i, l_i + e_j), \max(r_i, r_i + e_j)]$。因此我们可以这样求第二轮第 $i$ 步时的最大偏移量 $[l_i', r_i']$：

$$l_i'=\max (0, l_i+e_j-l_n)$$

$$r_i'=\max (0, r_i+e_j-r_n)$$

注意，这里的 $l_i'$ 和 $r_i'$ 是以第一轮后 $l_n$ 和 $r_n$ 为基准的，也就是说死去的点不能再死一次。这样在第二轮中死去的点有 $r_i'-l_i'$ 个。

我们可以发现，在第二轮及之后的死亡点的情况是相同的。因为第一轮中场上没有死去的点，死去的点不能再死一次。

有了这个发现就可以用周期来优化了。

设第一轮后剩下 $a_i$ 个起点，每轮会死掉 $b_i=r_n-l_n$ 个起点，最后一轮的前 $i$ 步会死掉 $f_i=r_i'-l_i'$ 个起点。这样第 $x+2$ 轮时的第 $i$ 步会剩下 $a_j-b_j\times x-f_i$ 个起点，贡献即为 $\prod _{j=1}^k (a_j-b_j\times x-f_{j, i})$。

我们设 $T = \min \frac{a_j-f_{j, i}}{b_j}$，也就是一共会进行的轮数，那么我们要算的式子就是：

$$\sum \limits_{i=1}^n\sum \limits_{u=1}^{T} \prod _{j=1}^k (a_j-b_j\times x-f_{j, i})$$

我们把里面的连乘展开，我们就能得到一个关于 $x$ 的多项式，我们发现 $x$ 的系数都与 $u$ 无关，我们把它提出去，就需要计算一个这个式子：$\sum_{u=1}^T x^u$。这个直接拉格朗日插值算就行了。而对于多项式的系数，我们直接背包即可。

时间复杂度 $O(nk^2)$。

2021

报数

设 $p(x)$ 表示 $x$ 的十进制表示中是否含有数字 $7$，若含有则 $p(x) = 1$，否则 $p(x) = 0$。则一个正整数 $x$ 不能被报出，当且仅当存在正整数 $y$ 和 $z$ ，使得 $x = yz$ 且 $p(y) = 1$。

多组询问，每次询问给定 $x$，求出 $x$ 下一个可以被报出的数字。

数据范围：$x\le 10^7, T\le 2\times 10^5$。

---

简单题，先用埃筛预处理一遍，然后再从后往前扫一遍，预处理出每一个数下一个能报的数。每次询问 $O(1)$ 即可。

时间复杂度 $O(n\log n + T)$。

数列

给定整数 $n, m, k$，和一个长度为 $m + 1$ 的正整数数组 $v_0, v_1, \ldots, v_m$。

对于一个长度为 $n$，下标从 $1$ 开始且每个元素均不超过 $m$ 的非负整数序列 $\{a_i\}$，我们定义它的权值为 $v_{a_1} \times v_{a_2} \times \cdots \times v_{a_n}$。

当这样的序列 $\{a_i\}$ 满足整数 $S = 2^{a_1} + 2^{a_2} + \cdots + 2^{a_n}$ 的二进制表示中 $1$ 的个数不超过 $k$ 时，我们认为 $\{a_i\}$ 是一个合法序列。

计算所有合法序列 $\{a_i\}$ 的权值和对 $998244353$ 取模的结果。

数据范围：$1 \leq k \leq n \leq 30$，$0 \leq m \leq 100$，$1 \leq v_i < 998244353$。

---

为什么 T2 就这么难啊/yiw

我们考虑这个 $S$ 的计算公式会涉及到低位到高位的进位，因此我们最好从低位开始 dp。又因为进位的问题，我们的状态里面应该设计一维用来记录进位。

因此我们设 $f[i,j,k,u]$ 为考虑前 $i$ 位，已经确定了 $j$ 个数，$S$ 中有 $k$ 个 $1$，当前位向高位进位 $u$ 时的权值和。转移我们就枚举第 $i$ 个数字选择多少即可。转移方程为：

$$f[i+1,j+t,k+(t+u)\bmod 2, \frac{t+u}{2}]\leftarrow f[i, j, k, u]\times v_{i}^t\times \dbinom{n-j}{t}$$

最后统计答案就看进位的数中 $1$ 的个数与 $k$ 的和是否超过限制即可。

时间复杂度 $O(n^4m)$。