本篇文章是为了总结一下最近做的组合数学的题目以及涉及到的知识点,以后可能会不定期补充。
同时也参考了大佬 lyt 的博客 。同时如果想要更深入地了解组合数学中的推式子技巧,可以看下 pjw 的博客。地址1 地址2
排列数 A n m A_n^m A n m n n n m m m A n m = n ! ( n − m ) ! A_n^m=\frac{n!}{(n-m)!} A n m = ( n − m ) ! n !
组合数(高中常用 C n m C_n^m C n m ( n m ) \dbinom{n}{m} ( m n ) n n n m m m ( n m ) = n ! m ! ( n − m ) ! \dbinom{n}{m} = \frac{n!}{m!(n-m)!} ( m n ) = m ! ( n − m ) ! n !
二项式定理:( x + y ) n = ∑ i = 0 n ( n i ) x i y n − i (x+y)^n=\sum \limits_{i=0}^n\dbinom{n}{i}x^iy^{n-i} ( x + y ) n = i = 0 ∑ n ( i n ) x i y n − i
( n m ) = ( n n − m ) \dbinom{n}{m} = \dbinom{n}{n-m} ( m n ) = ( n − m n ) ∑ i = 0 n ( n i ) = 2 n \sum \limits_{i=0}^n \dbinom{n}{i}=2^n i = 0 ∑ n ( i n ) = 2 n x = y = 1 x=y=1 x = y = 1 ∑ i = 0 n ( − 1 ) i ( n i ) = [ n = 0 ] \sum \limits_{i=0}^n (-1)^i\dbinom{n}{i}=[n=0] i = 0 ∑ n ( − 1 ) i ( i n ) = [ n = 0 ] x = 1 , y = − 1 x=1, y=-1 x = 1 , y = − 1 ( n m ) ( m k ) = ( n k ) ( n − k m − k ) \dbinom{n}{m}\dbinom{m}{k}=\dbinom{n}{k}\dbinom{n-k}{m-k} ( m n ) ( k m ) = ( k n ) ( m − k n − k ) ∑ i = 0 k ( n i ) ( m k − i ) = ( n + m k ) \sum \limits_{i=0}^k\dbinom{n}{i}\dbinom{m}{k-i}=\dbinom{n+m}{k} i = 0 ∑ k ( i n ) ( k − i m ) = ( k n + m ) ∑ i = 0 n ( i m ) = ( n + 1 m + 1 ) \sum \limits_{i=0}^n\dbinom{i}{m}=\dbinom{n+1}{m+1} i = 0 ∑ n ( m i ) = ( m + 1 n + 1 ) ( n m ) = ( n − 1 m − 1 ) + ( n − 1 m ) \dbinom{n}{m}=\dbinom{n-1}{m-1}+\dbinom{n-1}{m} ( m n ) = ( m − 1 n − 1 ) + ( m n − 1 )
设 f n f_n f n n n n g n g_n g n n n n i i i g n = ∑ i = 0 n ( n i ) f i g_n=\sum \limits _{i=0}^n\dbinom{n}{i}f_i g n = i = 0 ∑ n ( i n ) f i f n = ∑ i = 0 n ( − 1 ) n − i ( n i ) g i f_n=\sum \limits _{i=0}^n(-1)^{n-i}\dbinom{n}{i}g_i f n = i = 0 ∑ n ( − 1 ) n − i ( i n ) g i
(f i f_i f i g i g_i g i
证明如下(直接从十二重计数法那搬过来的)
∑ i = 0 n ( n i ) ( − 1 ) n − i f ( i ) = ∑ i = 0 n ( n i ) ( − 1 ) n − i ∑ j = 0 i ( i j ) g ( j ) = ∑ i = 0 n ∑ j = 0 i ( n i ) ( i j ) ( − 1 ) n − i g ( j ) = ∑ i = 0 n ∑ j = 0 i ( n j ) ( n − j i − j ) ( − 1 ) n − i g ( j ) = ∑ j = 0 n ( n j ) g ( j ) ∑ i = j n ( n − j i − j ) ( − 1 ) n − i = ∑ j = 0 n ( n j ) g ( j ) ∑ i = 0 n − j ( n − j i ) ( − 1 ) n − i − j = ∑ j = 0 n ( n j ) g ( j ) × 0 n − j = g ( n ) \begin{aligned}\sum \limits_{i=0}^n\dbinom{n}{i}(-1)^{n-i}f(i)&=\sum \limits_{i=0}^n\dbinom{n}{i}(-1)^{n-i} \sum \limits_{j=0}^i \dbinom{i}{j}g(j)\\&= \sum \limits_{i=0}^n \sum \limits_{j=0}^i\dbinom{n}{i}\dbinom{i}{j}(-1)^{n-i}g(j)\\&= \sum \limits_{i=0}^n\sum \limits_{j=0}^i \dbinom{n}{j}\dbinom{n-j}{i-j}(-1)^{n-i}g(j)\\&=\sum \limits_{j=0}^n \dbinom{n}{j}g(j)\sum \limits_{i=j}^n \dbinom{n-j}{i-j}(-1)^{n-i}\\&=\sum \limits_{j=0}^n \dbinom{n}{j}g(j)\sum \limits_{i=0}^{n-j} \dbinom{n-j}{i}(-1)^{n-i-j}\\&=\sum \limits_{j=0}^n \dbinom{n}{j}g(j)\times 0^{n-j}\\&= g(n)\end{aligned}
i = 0 ∑ n ( i n ) ( − 1 ) n − i f ( i ) = i = 0 ∑ n ( i n ) ( − 1 ) n − i j = 0 ∑ i ( j i ) g ( j ) = i = 0 ∑ n j = 0 ∑ i ( i n ) ( j i ) ( − 1 ) n − i g ( j ) = i = 0 ∑ n j = 0 ∑ i ( j n ) ( i − j n − j ) ( − 1 ) n − i g ( j ) = j = 0 ∑ n ( j n ) g ( j ) i = j ∑ n ( i − j n − j ) ( − 1 ) n − i = j = 0 ∑ n ( j n ) g ( j ) i = 0 ∑ n − j ( i n − j ) ( − 1 ) n − i − j = j = 0 ∑ n ( j n ) g ( j ) × 0 n − j = g ( n )
据说也可以用 EGF 证,但是我不会(
二项式反演的另一种常见形式:
设 f i f_i f i i i i g i g_i g i i i i i i i g k = ∑ i = k n ( i k ) f i g_k=\sum \limits _{i=k}^n\dbinom{i}{k}f_i g k = i = k ∑ n ( k i ) f i f k = ∑ i = k n ( − 1 ) i − k ( i k ) g i f_k=\sum \limits _{i=k}^n(-1)^{i-k}\dbinom{i}{k}g_i f k = i = k ∑ n ( − 1 ) i − k ( k i ) g i
(f i f_i f i g i g_i g i
同时,当 k = 0 k=0 k = 0 f 0 = ∑ i = 0 n ( − 1 ) i g i f_0=\sum \limits _{i=0}^n(-1)^{i}g_i f 0 = i = 0 ∑ n ( − 1 ) i g i
设多重集 S = { n 1 ⋅ x 1 , n 2 ⋅ x 2 , ⋯ , n k ⋅ x k } S=\{n_1\cdot x_1,n_2\cdot x_2, \cdots ,n_k\cdot x_k \} S = { n 1 ⋅ x 1 , n 2 ⋅ x 2 , ⋯ , n k ⋅ x k } n ! n 1 ! n 2 ! n 3 ! ⋯ n k ! ( n = ∑ n i ) \frac{n!}{n_1!n_2!n_3!\cdots n_k!}(n=\sum n_i) n 1 ! n 2 ! n 3 ! ⋯ n k ! n ! ( n = ∑ n i )
从集合 S = { n 1 ⋅ x 1 , n 2 ⋅ x 2 , ⋯ , n k ⋅ x k } S=\{n_1\cdot x_1,n_2\cdot x_2, \cdots ,n_k\cdot x_k \} S = { n 1 ⋅ x 1 , n 2 ⋅ x 2 , ⋯ , n k ⋅ x k } m m m
我们可以把问题转化成另一个形式:n 1 + n 2 + ⋯ + n k = m n_1+n_2+\cdots +n_k=m n 1 + n 2 + ⋯ + n k = m
多重集组合数分两种情况,没有上界和有上界。
先分析没有上界的情况,也就是 n i = ∞ n_i=\infty n i = ∞ ( m + k − 1 m − 1 ) \dbinom{m+k-1}{m-1} ( m − 1 m + k − 1 )
再分析有上界的情况。
当 ∀ i ∈ [ 1 , k ] , n i ≤ r i \forall i\in [1,k],n_i\le r_i ∀ i ∈ [ 1 , k ] , n i ≤ r i
公式太长了不放了
原始定义:C a t n = ∑ x + y = n − 1 C a t x C a t y Cat_n=\sum \limits _{x+y=n-1}Cat_xCat_y C a t n = x + y = n − 1 ∑ C a t x C a t y
递推公式:C a t n = 4 n − 2 n + 1 C a t n − 1 Cat_n=\frac{4n-2}{n+1} Cat_{n-1} C a t n = n + 1 4 n − 2 C a t n − 1
通项公式:C a t n = ( 2 n n ) − ( 2 n n + 1 ) Cat_n=\dbinom{2n}{n}-\dbinom{2n}{n+1} C a t n = ( n 2 n ) − ( n + 1 2 n )
以下问题的解均为卡特兰数:
大小为 n n n
凸 n + 2 n+2 n + 2
n n n 从 ( 0 , 0 ) (0,0) ( 0 , 0 ) ( n , n ) (n,n) ( n , n ) y = x y=x y = x
如果想要更详细的卡特兰数讲解,可以看 pjw 的博客 。这里不过多讲解。
设满足长度为 n n n ∀ i ∈ [ 1 , n ] , p i ≠ i \forall i\in [1,n],p_i\not= i ∀ i ∈ [ 1 , n ] , p i = i D n D_n D n D n = ( n − 1 ) ( D n − 1 + D n − 2 ) D_n=(n-1)(D_{n-1}+D_{n-2}) D n = ( n − 1 ) ( D n − 1 + D n − 2 ) D n = n D n − 1 + ( − 1 ) n D_n=n D_{n-1} + (-1)^{n} D n = n D n − 1 + ( − 1 ) n
我们设 f n f_n f n n n n g n g_n g n n n n g n = n ! g_n=n! g n = n ! f n = ∑ i = 0 n ( − 1 ) n − i ( n i ) i ! f_n=\sum \limits _{i=0}^n(-1)^{n-i}\dbinom{n}{i}i! f n = i = 0 ∑ n ( − 1 ) n − i ( i n ) i !
第二类斯特林数
第二类斯特林数 { n m } n\brace m { m n } n n n m m m
递推公式为 { n m } = { n − 1 m − 1 } + m { n − 1 m } {n\brace m}={n-1\brace m-1}+m{n-1\brace m} { m n } = { m − 1 n − 1 } + m { m n − 1 }
通项公式为:{ n m } = ∑ i = 0 m ( − 1 ) m − i i n i ! ( m − i ) ! {n\brace m}=\sum \limits _{i=0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!} { m n } = i = 0 ∑ m i ! ( m − i ) ! ( − 1 ) m − i i n
m n = ∑ i = 0 m o r n { n i } i ! ( m i ) m^n= \sum \limits _{i=0}^{m\ \mathrm{or} \ n}{n\brace i}i!\dbinom{m}{i}
m n = i = 0 ∑ m o r n { i n } i ! ( i m )
可以类比十二重计数法中的情况,m n m^n m n n n n m m m i i i i ! i! i ! x k x^k x k
∑ i = 0 n i k = ∑ i = 0 n ∑ j = 0 k { k j } j ! ( i j ) = ∑ j = 0 k { k j } j ! ∑ i = 0 n ( i j ) = ∑ j = 0 k { k j } j ! ( n + 1 j + 1 ) \begin{aligned}
\sum \limits_{i=0}^n i^k&=\sum \limits_{i=0}^{n} \sum \limits _{j=0}^k {k\brace j}j!\dbinom{i}{j} \\
&=\sum \limits _{j=0}^k{k\brace j}j! \sum \limits _{i=0}^n \dbinom{i}{j}\\
&= \sum \limits _{j=0}^k{k\brace j}j!\dbinom{n+1}{j+1}
\end{aligned}
i = 0 ∑ n i k = i = 0 ∑ n j = 0 ∑ k { j k } j ! ( j i ) = j = 0 ∑ k { j k } j ! i = 0 ∑ n ( j i ) = j = 0 ∑ k { j k } j ! ( j + 1 n + 1 )
我们也可以得到自然数幂求和的一个结论:
∑ i = 0 n i k = ∑ i = 0 n ∑ j = 0 k { k j } j ! ( i j ) = ∑ j = 0 k { k j } j ! ∑ i = 0 n ( i j ) = ∑ j = 0 k { k j } j ! ( n + 1 j + 1 ) \begin{aligned}
\sum \limits _{i = 0}^ni^k & = \sum \limits _{i = 0}^n\sum \limits _{j = 0}^k {k \brace j}j!\dbinom{i}{j}\\
&= \sum \limits _{j=0}^k{k\brace j}j!\sum \limits _{i=0}^n\dbinom{i}{j}\\
&= \sum \limits _{j=0}^k{k\brace j}j!\dbinom{n+1}{j+1}
\end{aligned}
i = 0 ∑ n i k = i = 0 ∑ n j = 0 ∑ k { j k } j ! ( j i ) = j = 0 ∑ k { j k } j ! i = 0 ∑ n ( j i ) = j = 0 ∑ k { j k } j ! ( j + 1 n + 1 )
第一类斯特林数
第一类斯特林数 [ n m ] {n\brack m} [ m n ] n n n m m m 1 , 2 , 3 , 4 , 5 1,2,3,4,5 1 , 2 , 3 , 4 , 5 5 , 1 , 2 , 3 , 4 5,1,2,3,4 5 , 1 , 2 , 3 , 4
递推公式:[ n m ] = [ n − 1 m − 1 ] + ( n − 1 ) [ n − 1 m ] {n\brack m}={n-1\brack m-1}+(n-1){n-1\brack m} [ m n ] = [ m − 1 n − 1 ] + ( n − 1 ) [ m n − 1 ]
第一类斯特林数没有实用的通项公式。
本来这里想咕掉不写斯特林的一些科技的,直到我发现 2020 年省选考了下降幂
上升幂与下降幂
下降幂:x n ‾ = x ! ( x − n ) ! = ∏ i = 0 n − 1 ( x − i ) x^{\underline{n}}=\frac{x!}{(x-n)!} = {\prod_{i=0}^{n-1}(x-i)} x n = ( x − n ) ! x ! = ∏ i = 0 n − 1 ( x − i )
上升幂:x n ˉ = ∏ i = 0 n − 1 ( x + i ) x^{\bar{n}}={\prod_{i=0}^{n-1}(x+i)} x n ˉ = ∏ i = 0 n − 1 ( x + i )
下降幂性质:m k ‾ ( n m ) = ( n − k m − k ) n k ‾ m^{\underline{k}}\dbinom{n}{m} = \dbinom{n-k}{m-k}n^{\underline{k}} m k ( m n ) = ( m − k n − k ) n k
证明:
m k ‾ ( n m ) = m ! ( m − k ) ! n ! m ! ( n − m ) ! = ( n − k ) ! ( m − k ) ! ( n − m ) ! n ! ( n − k ) ! = ( n − k m − k ) n k ‾ \begin{aligned}
m^{\underline{k}}\dbinom{n}{m} &= \frac{m!}{(m-k)!}\frac{n!}{m!(n-m)!} \\
&=\frac{(n-k)!}{(m-k)!(n-m)!}\frac{n!}{(n-k)!}\\
&=\dbinom{n-k}{m-k}n^{\underline{k}}
\end{aligned}
m k ( m n ) = ( m − k ) ! m ! m ! ( n − m ) ! n ! = ( m − k ) ! ( n − m ) ! ( n − k ) ! ( n − k ) ! n ! = ( m − k n − k ) n k
下降幂上升幂互换:x n ‾ = ( − 1 ) n ( − x ) n ˉ x^{\underline{n}}=(-1)^n(-x)^{\bar{n}} x n = ( − 1 ) n ( − x ) n ˉ
普通幂转下降幂:x n = ∑ i = 0 n { n i } x i ‾ x^n=\sum \limits _{i=0}^n {n\brace i}x^{\underline{i}} x n = i = 0 ∑ n { i n } x i x n ‾ = ∑ i = 0 n ( − 1 ) n − i [ n i ] x i x^{\underline{n}}=\sum \limits _{i=0}^n (-1)^{n-i}{n\brack i}x^{i} x n = i = 0 ∑ n ( − 1 ) n − i [ i n ] x i
普通幂转上升幂:x n = ∑ i = 0 n ( − 1 ) n − i { n i } x i ˉ x^{n}=\sum \limits _{i=0}^n (-1)^{n-i}{n\brace i}x^{\bar{i}} x n = i = 0 ∑ n ( − 1 ) n − i { i n } x i ˉ x n ˉ = ∑ i = 0 n [ n i ] x i x^{\bar{n}}=\sum \limits _{i=0}^n {n\brack i}x^{i} x n ˉ = i = 0 ∑ n [ i n ] x i
对第二个式子和第四个式子的证明:
第二个式子:
考虑数学归纳法
x n + 1 ‾ = ( x − n ) x n ‾ = ( x − n ) ∑ i = 0 n ( − 1 ) n − i [ n i ] x i = x ∑ i = 0 n ( − 1 ) n − i [ n i ] x i − n ∑ i = 0 n ( − 1 ) n − i [ n i ] x i = ∑ i = 0 n ( − 1 ) n − i [ n i ] x i + 1 − n ∑ i = 0 n + 1 ( − 1 ) n − i [ n i ] x i = ∑ i = 1 n + 1 ( − 1 ) n − i + 1 [ n i − 1 ] x i + n ∑ i = 1 n + 1 ( − 1 ) n − i + 1 [ n i ] x i = ∑ i = 1 n + 1 ( [ n i − 1 ] + n [ n i ] ) ( − 1 ) n − i + 1 x i = ∑ i = 1 n + 1 [ n + 1 i ] ( − 1 ) n + 1 − i x i = ∑ i = 0 n + 1 [ n + 1 i ] ( − 1 ) n + 1 − i x i \begin{aligned}x^{\underline{n+1}}&=(x-n)x^{\underline{n}}\\&=(x-n)\sum \limits _{i=0}^n (-1)^{n-i}{n\brack i}x^{i}\\&=x\sum \limits _{i=0}^n (-1)^{n-i}{n\brack i}x^{i}-n\sum \limits _{i=0}^n (-1)^{n-i}{n\brack i}x^{i}\\&=\sum \limits _{i=0}^n (-1)^{n-i}{n\brack i}x^{i+1}-n\sum \limits _{i=0}^{n+1} (-1)^{n-i}{n\brack i}x^{i}\\&=\sum \limits _{i=1}^{n+1} (-1)^{n-i+1}{n\brack i-1}x^{i}+n\sum \limits _{i=1}^{n+1} (-1)^{n-i+1}{n\brack i}x^{i}\\&=\sum \limits _{i=1}^{n+1}({n\brack i-1}+n{n\brack i})(-1)^{n-i+1}x^i\\&=\sum \limits _{i=1}^{n+1}{n+1\brack i}(-1)^{n+1-i}x^i\\&=\sum \limits _{i=0}^{n+1}{n+1\brack i}(-1)^{n+1-i}x^i\end{aligned}
x n + 1 = ( x − n ) x n = ( x − n ) i = 0 ∑ n ( − 1 ) n − i [ i n ] x i = x i = 0 ∑ n ( − 1 ) n − i [ i n ] x i − n i = 0 ∑ n ( − 1 ) n − i [ i n ] x i = i = 0 ∑ n ( − 1 ) n − i [ i n ] x i + 1 − n i = 0 ∑ n + 1 ( − 1 ) n − i [ i n ] x i = i = 1 ∑ n + 1 ( − 1 ) n − i + 1 [ i − 1 n ] x i + n i = 1 ∑ n + 1 ( − 1 ) n − i + 1 [ i n ] x i = i = 1 ∑ n + 1 ( [ i − 1 n ] + n [ i n ] ) ( − 1 ) n − i + 1 x i = i = 1 ∑ n + 1 [ i n + 1 ] ( − 1 ) n + 1 − i x i = i = 0 ∑ n + 1 [ i n + 1 ] ( − 1 ) n + 1 − i x i
第四个式子可以把上升幂转下降幂,再用第二个式子的结论。
x n ˉ = ( − 1 ) n ( − x ) n ‾ = ∑ i = 0 n [ n i ] ( − 1 ) n ( − 1 ) n − i ( − x ) i = ∑ i = 0 n [ n i ] x i \begin{aligned}
x^{\bar{n}} &= (-1)^n(-x)^{\underline{n}}\\
&=\sum \limits _{i=0}^n{n\brack i} (-1)^n (-1)^{n-i} (-x)^i\\
&=\sum \limits _{i=0}^n{n\brack i}x^i
\end{aligned}
x n ˉ = ( − 1 ) n ( − x ) n = i = 0 ∑ n [ i n ] ( − 1 ) n ( − 1 ) n − i ( − x ) i = i = 0 ∑ n [ i n ] x i
斯特林反演
若 g n = ∑ i = 0 n { n i } f i g_n=\sum \limits _{i=0}^n{n\brace i}f_i g n = i = 0 ∑ n { i n } f i f n = ∑ i = 0 n ( − 1 ) n − i [ n i ] g i f_n=\sum \limits _{i=0}^n (-1)^{n-i}{n\brack i}g_i f n = i = 0 ∑ n ( − 1 ) n − i [ i n ] g i
斯特林反演不太常用,可以暂时不掌握。
组合数学不是会数数就行吗
[SDOI2016] 排列计数
求有多少种 1 ∼ n 1 \sim n 1 ∼ n m m m a i = i a_i=i a i = i
数据范围:T ≤ 5 × 1 0 5 , n , m ≤ 1 × 1 0 6 T \le 5\times 10^5, n, m\le 1 \times 10^6 T ≤ 5 × 1 0 5 , n , m ≤ 1 × 1 0 6
原排列除去这 m m m n n n m m m D n − m ( n m ) D_{n-m}\dbinom{n}{m} D n − m ( m n ) O ( T + n ) O(T+n) O ( T + n )
[NOI Online #2 入门组] 建设城市
求满足以下条件的长度为 2 n 2n 2 n a a a m m m n n n n n n a x = a y a_x=a_y a x = a y
数据范围:n ≤ 2 × 1 0 5 n \le 2\times 10^5 n ≤ 2 × 1 0 5
我们可以枚举 x x x i i i
当 x ≤ n ≤ y x \le n \le y x ≤ n ≤ y x , y x, y x , y [ 1 , x − 1 ] [1,x-1] [ 1 , x − 1 ] [ 1 , x − 1 ] [1,x-1] [ 1 , x − 1 ] ( x − 1 + i − 1 i − 1 ) \dbinom{x-1+i-1}{i-1} ( i − 1 x − 1 + i − 1 )
当 x < y < n x < y < n x < y < n n < x < y n < x < y n < x < y x ∼ y x\sim y x ∼ y
时间复杂度 O ( n ) O(n) O ( n )
[HAOI2011]Problem c
有 n n n a i a_i a i 1 ∼ n 1\sim n 1 ∼ n a i + 1 , a i + 2 a_i + 1, a_i + 2 a i + 1 , a i + 2 n n n m m m
数据范围:n ≤ 300 n \le 300 n ≤ 3 0 0
首先考虑无解的情况,我们设 s u m i sum_i s u m i i i i s u m i > n − i + 1 sum_i > n - i + 1 s u m i > n − i + 1 f i , j f_{i, j} f i , j i i i j j j k k k k k k i i i f i , j = ∑ k = 0 j ( j k ) f i + 1 , j − k ( 0 ≤ j ≤ n − i + 1 − s u m i ) f_{i,j}=\sum \limits _{k=0}^j \dbinom{j}{k} f_{i+1,j-k}(0\le j \le n-i+1-sum_i) f i , j = k = 0 ∑ j ( k j ) f i + 1 , j − k ( 0 ≤ j ≤ n − i + 1 − s u m i ) f 1 , n − m f_{1, n-m} f 1 , n − m
[SHOI2015]超能粒子炮·改
求 ∑ i = 0 k ( n i ) m o d 2333 \sum \limits _{i=0}^k\dbinom{n}{i}\bmod 2333 i = 0 ∑ k ( i n ) m o d 2 3 3 3
设 f n , k = ∑ i = 0 k ( n i ) m o d 2333 f_{n, k} = \sum \limits _{i=0}^k\dbinom{n}{i}\bmod 2333 f n , k = i = 0 ∑ k ( i n ) m o d 2 3 3 3
开始大力推式子
f n , k = ∑ i = 0 k ( n i ) m o d p = ∑ i = 0 k ( n / p i / p ) ( n m o d p i m o d p ) = ( n / p 0 ) ∑ i = 0 p − 1 ( n m o d p i ) + ( n / p 1 ) ∑ i = 0 p − 1 ( n m o d p i ) + ⋯ + ( n / p k / p − 1 ) ∑ i = 0 p − 1 ( n m o d p i ) + ( n / p k / p ) ∑ i = 0 k m o d p ( n m o d p i ) = ∑ i = 0 p − 1 ( n m o d p i ) × ∑ i = 0 k / p − 1 ( n / p i ) + ( n / p k / p ) ∑ i = 0 k m o d p ( n m o d p i ) = f n m o d p , p − 1 × f n / p , k / p − 1 + ( n / p k / p ) f n m o d p , k m o d p \begin{aligned}
f_{n,k}&=\sum\limits _{i=0}^k \dbinom{n}{i}\bmod p\\
&=\sum \limits _{i=0}^k\dbinom{n/p}{i/p}\dbinom{n\bmod p}{i \bmod p}\\
&=\dbinom{n/p}{0}\sum \limits_{i=0}^{p-1}\dbinom{n\bmod p}{i} +\dbinom{n/p}{1}\sum \limits_{i=0}^{p-1}\dbinom{n\bmod p}{i}+\cdots+\dbinom{n/p}{k/p-1}\sum \limits_{i=0}^{p-1}\dbinom{n\bmod p}{i}+\dbinom{n/p}{k/p}\sum \limits_{i=0}^{k \bmod p}\dbinom{n\bmod p}{i}\\
&=\sum \limits _{i=0}^{p-1}\dbinom{n \bmod p}{i}\times\sum \limits_{i=0}^{k/p-1}\dbinom{n/p}{i}+\dbinom{n/p}{k/p}\sum \limits_{i=0}^{k \bmod p}\dbinom{n\bmod p}{i}\\
&=f_{n \bmod p, p-1}\times f_{n/p, k/p-1}+\dbinom{n/p}{k/p} f_{n \bmod p, k \bmod p}
\end{aligned}
f n , k = i = 0 ∑ k ( i n ) m o d p = i = 0 ∑ k ( i / p n / p ) ( i m o d p n m o d p ) = ( 0 n / p ) i = 0 ∑ p − 1 ( i n m o d p ) + ( 1 n / p ) i = 0 ∑ p − 1 ( i n m o d p ) + ⋯ + ( k / p − 1 n / p ) i = 0 ∑ p − 1 ( i n m o d p ) + ( k / p n / p ) i = 0 ∑ k m o d p ( i n m o d p ) = i = 0 ∑ p − 1 ( i n m o d p ) × i = 0 ∑ k / p − 1 ( i n / p ) + ( k / p n / p ) i = 0 ∑ k m o d p ( i n m o d p ) = f n m o d p , p − 1 × f n / p , k / p − 1 + ( k / p n / p ) f n m o d p , k m o d p
我们就可以递推出前 2333 2333 2 3 3 3 f f f
[CQOI2018]交错序列
交错序列的定义是:只由 0 0 0 1 1 1 1 1 1 0 0 0 x x x 1 1 1 y y y x a y b x^ay^b x a y b a , b a, b a , b n n n
数据范围:n ≤ 1 0 7 n \le 10^7 n ≤ 1 0 7
我们枚举 1 1 1 x x x 1 1 1 n − x n-x n − x 0 0 0 n − x + 1 n-x+1 n − x + 1 x x x 1 1 1 ( n − x + 1 x ) \dbinom{n-x+1}{x} ( x n − x + 1 ) i a i^a i a i b i^b i b O ( n ) O(n) O ( n )
Anton and School - 2
给定一个长度为 n n n (,右半部分为 )。
数据范围:n ≤ 2 × 1 0 5 n \le 2\times 10^5 n ≤ 2 × 1 0 5
我们枚举每一个 (,在它左边有 a a a ((包括它自己),右边有 b b b )。那么它对答案的贡献为 ∑ i = 0 min ( a − 1 , b − 1 ) ( a − 1 i ) ( b i + 1 ) \sum \limits _{i=0}^{\min(a-1, b-1)}\dbinom{a-1}{i}\dbinom{b}{i+1} i = 0 ∑ m i n ( a − 1 , b − 1 ) ( i a − 1 ) ( i + 1 b ) ∑ i = 0 k ( n i ) ( m k − i ) = ( n + m k ) \sum \limits _{i=0}^k\dbinom{n}{i}\dbinom{m}{k-i}=\dbinom{n+m}{k} i = 0 ∑ k ( i n ) ( k − i m ) = ( k n + m )
我们把上面的 min \min min a ≤ b a\le b a ≤ b
∑ i = 0 a − 1 ( a − 1 i ) ( b i + 1 ) = ∑ i = 0 a − 1 ( a − 1 a − 1 − i ) ( b i + 1 ) = ∑ i = 0 a ( a − 1 a − 1 − i ) ( b i + 1 ) = ( a + b − 1 a ) \begin{aligned}
\sum \limits _{i= 0}^{a-1}\dbinom{a-1}{i}\dbinom{b}{i+1} & = \sum \limits _{i = 0}^{a-1}\dbinom{a-1}{a-1-i}\dbinom{b}{i+1}\\
& = \sum \limits _{i = 0}^{a}\dbinom{a-1}{a-1-i}\dbinom{b}{i+1}\\
& = \dbinom{a+b-1}{a}
\end{aligned}
i = 0 ∑ a − 1 ( i a − 1 ) ( i + 1 b ) = i = 0 ∑ a − 1 ( a − 1 − i a − 1 ) ( i + 1 b ) = i = 0 ∑ a ( a − 1 − i a − 1 ) ( i + 1 b ) = ( a a + b − 1 )
当 b ≤ a b \le a b ≤ a
∑ i = 0 b − 1 ( a − 1 i ) ( b i + 1 ) = ∑ i = 0 b − 1 ( a − 1 i ) ( b b − 1 − i ) = ( a + b − 1 b − 1 ) = ( a + b − 1 a ) \begin{aligned}
\sum \limits _{i= 0}^{b-1}\dbinom{a-1}{i}\dbinom{b}{i+1} & = \sum \limits _{i = 0}^{b-1}\dbinom{a-1}{i}\dbinom{b}{b-1-i}\\
& = \dbinom{a+b-1}{b-1}\\
&=\dbinom{a+b-1}{a}
\end{aligned}
i = 0 ∑ b − 1 ( i a − 1 ) ( i + 1 b ) = i = 0 ∑ b − 1 ( i a − 1 ) ( b − 1 − i b ) = ( b − 1 a + b − 1 ) = ( a a + b − 1 )
因此对答案的贡献即为 ( a + b − 1 a ) \dbinom{a+b-1}{a} ( a a + b − 1 ) O ( n ) O(n) O ( n )
梦现时刻
设 f a , b = ∑ i = 0 b ( b i ) ( n − i a ) f_{a,b}=\sum \limits _{i=0}^b\dbinom{b}{i}\dbinom{n-i}{a} f a , b = i = 0 ∑ b ( i b ) ( a n − i ) ⊕ a = 1 m ⊕ b = 1 m f a , b m o d 998244353 \oplus _{a=1}^m\oplus_{b=1}^m f_{a,b} \bmod 998244353 ⊕ a = 1 m ⊕ b = 1 m f a , b m o d 9 9 8 2 4 4 3 5 3
其中 ⊕ \oplus ⊕
数据范围:1 ≤ n ≤ 1 0 0 , m ≤ 5000 1 \le n \le 10^0, m \le 5000 1 ≤ n ≤ 1 0 0 , m ≤ 5 0 0 0
比较牛逼的推式子题。
f a , b = ∑ i = 0 b ( b i ) ( n − i a ) = ∑ i = 0 b ( b − 1 i ) ( n − i a ) + ∑ i = 0 b ( b − 1 i − 1 ) ( n − i a ) = f a , b − 1 + ∑ i = 0 b − 1 ( b − 1 i ) ( n − i − 1 a ) = f a , b − 1 + ∑ i = 0 b − 1 ( b − 1 i ) ( n − i a ) − ∑ i = 0 b − 1 ( b − 1 i ) ( n − i − 1 a − 1 ) = 2 f a , b − 1 − ∑ i = 0 b − 1 ( b − 1 i ) ( n − i − 1 a − 1 ) = 2 f a , b − 1 − ( ∑ i = 0 b − 1 ( b i + 1 ) ( n − i − 1 a − 1 ) − ∑ i = 0 b − 1 ( b − 1 i + 1 ) ( n − i − 1 a − 1 ) ) = 2 f a , b − 1 − ∑ i = 0 b ( b i ) ( n − i a − 1 ) + ∑ i = 0 b ( b − 1 i ) ( n − i a − 1 ) = 2 f a , b − 1 − f a − 1 , b + f a − 1 , b − 1 \begin{aligned}f_{a,b} & = \sum \limits _{i = 0}^b\dbinom{b}{i}\dbinom{n-i}{a} \\&=\sum \limits _{i=0}^b\dbinom{b-1}{i}\dbinom{n-i}{a}+\sum \limits _{i=0}^b\dbinom{b-1}{i-1}\dbinom{n-i}{a}\\&=f_{a,b-1}+\sum \limits _{i=0}^{b-1}\dbinom{b-1}{i}\dbinom{n-i-1}{a}\\&=f_{a,b-1}+\sum \limits _{i=0}^{b-1}\dbinom{b-1}{i}\dbinom{n-i}{a}-\sum \limits _{i=0}^{b-1}\dbinom{b-1}{i}\dbinom{n-i-1}{a-1}\\&=2f_{a,b-1}-\sum \limits _{i=0}^{b-1}\dbinom{b-1}{i}\dbinom{n-i-1}{a-1}\\&=2f_{a,b-1}-(\sum \limits _{i=0}^{b-1}\dbinom{b}{i+1}\dbinom{n-i-1}{a-1}-\sum \limits _{i=0}^{b-1}\dbinom{b-1}{i+1}\dbinom{n-i-1}{a-1})\\&=2f_{a,b-1}-\sum \limits _{i=0}^{b}\dbinom{b}{i}\dbinom{n-i}{a-1}+\sum \limits _{i=0}^{b}\dbinom{b-1}{i}\dbinom{n-i}{a-1}\\&=2f_{a,b-1}-f_{a-1,b}+f_{a-1,b-1}\end{aligned}
f a , b = i = 0 ∑ b ( i b ) ( a n − i ) = i = 0 ∑ b ( i b − 1 ) ( a n − i ) + i = 0 ∑ b ( i − 1 b − 1 ) ( a n − i ) = f a , b − 1 + i = 0 ∑ b − 1 ( i b − 1 ) ( a n − i − 1 ) = f a , b − 1 + i = 0 ∑ b − 1 ( i b − 1 ) ( a n − i ) − i = 0 ∑ b − 1 ( i b − 1 ) ( a − 1 n − i − 1 ) = 2 f a , b − 1 − i = 0 ∑ b − 1 ( i b − 1 ) ( a − 1 n − i − 1 ) = 2 f a , b − 1 − ( i = 0 ∑ b − 1 ( i + 1 b ) ( a − 1 n − i − 1 ) − i = 0 ∑ b − 1 ( i + 1 b − 1 ) ( a − 1 n − i − 1 ) ) = 2 f a , b − 1 − i = 0 ∑ b ( i b ) ( a − 1 n − i ) + i = 0 ∑ b ( i b − 1 ) ( a − 1 n − i ) = 2 f a , b − 1 − f a − 1 , b + f a − 1 , b − 1
直接 O ( n 2 ) O(n^2) O ( n 2 )
[AGC002F] Leftmost Ball
给你 n n n k k k n × k n\times k n × k
数据范围:1 ≤ n , k ≤ 2000 1\leq n, k\leq 2000 1 ≤ n , k ≤ 2 0 0 0
合法的情况为:在任意前缀中,白球的种类都大于等于其他颜色的种类。
设 f i , j f_{i, j} f i , j i i i j j j
为了防止方案重复,我们规定,每次放球时,必须将球放到第一个空位上。
考虑最左边的第一个空位放什么球。当放白球时,可以从 f i − 1 , j f_{i-1,j} f i − 1 , j
当放其他颜色的球时,可以从 f i , j + 1 f_{i, j+1} f i , j + 1 n − j + 1 n-j+1 n − j + 1 k − 2 k-2 k − 2 f i , j = f i − 1 , j + f i , j − 1 × ( n − j + 1 ) × ( n k − i − ( j − 1 ) ( k − 1 ) − 1 k − 2 ) f_{i,j}=f_{i-1,j}+f_{i,j-1}\times (n-j+1)\times \dbinom{nk-i-(j-1)(k-1)-1}{k-2} f i , j = f i − 1 , j + f i , j − 1 × ( n − j + 1 ) × ( k − 2 n k − i − ( j − 1 ) ( k − 1 ) − 1 )
时间复杂度为 O ( n 2 ) O(n^2) O ( n 2 )
硬币购物
有四种面值为 c 1 , c 2 , c 3 , c 4 c_1,c_2,c_3,c_4 c 1 , c 2 , c 3 , c 4 T T T l i m 1 , l i m 2 , l i m 3 , l i m 4 , t o t lim_1,lim_2,lim_3,lim_4,tot l i m 1 , l i m 2 , l i m 3 , l i m 4 , t o t i i i l i m i lim_i l i m i t o t tot t o t
数据范围:T ≤ 1000 T \le 1000 T ≤ 1 0 0 0
先做一遍完全背包,求出没有限制时凑出面值 t t t O ( 16 T ) O(16T) O ( 1 6 T )
[CSP-S2019] Emiya 家今天的饭
有 n n n m m m i i i j j j a i , j a_{i,j} a i , j
数据范围:n ≤ 100 , m ≤ 2 × 1 0 3 n \le 100, m \le 2 \times 10^3 n ≤ 1 0 0 , m ≤ 2 × 1 0 3
考虑容斥,让一种菜超出一半的限制,再用总方案减去即可。考虑求出总方案。设 f i , j f_{i, j} f i , j i i i j j j s i s_i s i ∑ j = 1 m a j \sum_{j=1}^m a_j ∑ j = 1 m a j f i , j = f i − 1 , j + s i × f i − 1 , j − 1 f_{i,j}=f_{i-1,j}+s_i\times f_{i-1,j-1} f i , j = f i − 1 , j + s i × f i − 1 , j − 1 ∑ i = 1 n f n , i \sum_{i=1}^n f_{n,i} ∑ i = 1 n f n , i p p p g i , j , k g_{i, j, k} g i , j , k i i i p p p j j j k k k p p p g i , j , k = g i − 1 , j , k + a i , p g i − 1 , j − 1 , k + ( s i − a i , p ) g i − 1 , j , k − 1 g_{i, j, k} = g_{i-1,j,k}+a_{i,p}g_{i-1,j-1,k}+(s_i-a_{i,p})g_{i-1,j,k-1} g i , j , k = g i − 1 , j , k + a i , p g i − 1 , j − 1 , k + ( s i − a i , p ) g i − 1 , j , k − 1 O ( m n 3 ) O(mn^3) O ( m n 3 ) j j j k k k g i , j g_{i,j} g i , j i i i p p p j j j g i , j = g i − 1 , j + a i , p g i − 1 , j − 1 + ( s i − a i , p ) g i − 1 , j + 1 g_{i, j} = g_{i-1,j}+a_{i,p}g_{i-1,j-1}+(s_i-a_{i,p})g_{i-1,j+1} g i , j = g i − 1 , j + a i , p g i − 1 , j − 1 + ( s i − a i , p ) g i − 1 , j + 1 O ( m n 2 ) O(mn^2) O ( m n 2 )
[HNOI2011] 卡农
从集合 S = { 1 , 2 , 3 ⋯ n } S=\{ 1, 2, 3\cdots n\} S = { 1 , 2 , 3 ⋯ n } m m m
数据范围:n ≤ 1 0 6 n \le 10^6 n ≤ 1 0 6
我们可以把题意转化为:有 2 n − 1 2^n-1 2 n − 1 m m m 0 0 0 m ! m! m ! f i f_i f i i i i 0 0 0 A 2 n − 1 i − 1 A_{2^n-1}^{i-1} A 2 n − 1 i − 1 i − 1 i-1 i − 1 x x x x x x x = 0 x=0 x = 0 i − 1 i-1 i − 1 x x x x x x 0 0 0 i − 2 i-2 i − 2 x x x 2 n − 1 − ( i − 2 ) 2^n-1-(i-2) 2 n − 1 − ( i − 2 ) x x x i − 1 i-1 i − 1 f i = A 2 n − 1 i − 1 − f i − 1 − f i − 2 × ( 2 n − i + 1 ) × ( i − 1 ) f_i=A_{2^n-1}^{i-1}-f_{i-1}-f_{i-2}\times (2^n-i+1)\times (i-1) f i = A 2 n − 1 i − 1 − f i − 1 − f i − 2 × ( 2 n − i + 1 ) × ( i − 1 ) f m m ! \frac{f_m}{m!} m ! f m
[HAOI2018]染色
有一个长度为 n n n m m m s s s k k k s s s w k w_k w k 1004535809 1004535809 1 0 0 4 5 3 5 8 0 9
1004535809 1004535809 1 0 0 4 5 3 5 8 0 9 3 3 3
我们设 f i f_i f i s s s i i i g i g_i g i s s s i i i g i g_i g i m m m i i i n − i s n-is n − i s n ! ( s ! ) i ( n − i s ) ! \frac{n!}{(s!)^i(n-is)!} ( s ! ) i ( n − i s ) ! n ! m − i m-i m − i n − i s n-is n − i s ( m − i ) n − i s (m-i)^{n-is} ( m − i ) n − i s g i = ( m i ) n ! ( s ! ) i ( n − i s ) ! ( m − i ) n − i s g_i=\dbinom{m}{i} \frac{n!}{(s!)^i(n-is)!} (m-i)^{n-is} g i = ( i m ) ( s ! ) i ( n − i s ) ! n ! ( m − i ) n − i s
再考虑求出 f k f_k f k u p = min ( m , ⌊ n s ⌋ ) up = \min(m,\left \lfloor \frac{n}{s} \right \rfloor) u p = min ( m , ⌊ s n ⌋ )
f k = ∑ i = k u p ( − 1 ) i − k ( i k ) g i = ∑ i = k u p ( − 1 ) i − k i ! ( i − k ) ! k ! g i = 1 k ! ∑ i = k u p ( − 1 ) i − k ( i − k ) ! ( i ! g i ) \begin{aligned}
f_k & = \sum \limits _{i = k}^{up}(-1)^{i-k}\dbinom{i}{k}g_i\\
&= \sum \limits _{i = k}^{up}\frac{(-1)^{i-k}i!}{(i-k)!k!} g_i\\
&=\frac{1}{k!} \sum \limits _{i = k}^{up}\frac{(-1)^{i-k}}{(i-k)!}(i!g_i)
\end{aligned}
f k = i = k ∑ u p ( − 1 ) i − k ( k i ) g i = i = k ∑ u p ( i − k ) ! k ! ( − 1 ) i − k i ! g i = k ! 1 i = k ∑ u p ( i − k ) ! ( − 1 ) i − k ( i ! g i )
设 F ( x ) = ∑ i = 0 u p ( − 1 ) i i ! x i , G ( x ) = ∑ i = 0 u p i ! × g i × x i F(x)=\sum \limits_{i=0}^{up}\frac{(-1)^i}{i!}x^i,G(x)=\sum \limits_{i=0}^{up}i!\times g_i\times x^i F ( x ) = i = 0 ∑ u p i ! ( − 1 ) i x i , G ( x ) = i = 0 ∑ u p i ! × g i × x i f k = 1 k ! ∑ i = k u p F i − k G i f_k=\frac{1}{k!} \sum \limits_{i=k}^{up}F_{i-k}G_{i} f k = k ! 1 i = k ∑ u p F i − k G i O ( m log m ) O(m\log m) O ( m log m )
[JSOI2011]分特产
有 m m m a i a_i a i n n n
数据范围:n , m , a i ≤ 1000 n, m, a_i \le 1000 n , m , a i ≤ 1 0 0 0
设 g i g_i g i i i i g i = ( n i ) ∏ j = 1 m ( a j + n − i − 1 n − i − 1 ) g_i=\dbinom{n}{i} \prod_{j=1}^{m}\dbinom{a_j+n-i-1}{n-i-1} g i = ( i n ) ∏ j = 1 m ( n − i − 1 a j + n − i − 1 ) a n s = ∑ i = 0 n ( − 1 ) i g i ans = \sum_{i=0}^n (-1)^i g_i a n s = ∑ i = 0 n ( − 1 ) i g i O ( n m ) O(nm) O ( n m )
[TJOI2019]唱、跳、rap和篮球
现在有 a a a A,b b b B,c c c C,d d d D,要求把这些字母中的 n n n n n n ABCD。求合法方案数对 998244353 998244353 9 9 8 2 4 4 3 5 3
数据范围:n ≤ 1000 , a , b , c , d ≤ 500 n \le 1000, a,b,c,d \le 500 n ≤ 1 0 0 0 , a , b , c , d ≤ 5 0 0
考虑二项式反演,设 g i g_i g i i i i ABCD 的方案,我们先把这 i i i n − 4 i n-4i n − 4 i g i g_i g i g i g_i g i h n , a , b , c , d h_{n,a,b,c,d} h n , a , b , c , d a a a A,b b b B,c c c C,d d d D 的情况下在 n n n g i = ( n − 3 i i ) h n − 4 i , a − i , b − i , c − i , d − i g_i=\dbinom{n-3i}{i}h_{n-4i,a-i,b-i,c-i,d-i} g i = ( i n − 3 i ) h n − 4 i , a − i , b − i , c − i , d − i h h h h n , a , b , c , d = ∑ p = 0 a ∑ q = 0 b ∑ s = 0 c ∑ t = 0 d n ! p ! q ! s ! t ! [ p + q + s + t = n ] h_{n,a,b,c,d}=\sum\limits_{p=0}^a\sum\limits_{q=0}^b\sum\limits_{s=0}^c\sum\limits_{t=0}^d \frac{n!}{p!q!s!t!}[p+q+s+t=n] h n , a , b , c , d = p = 0 ∑ a q = 0 ∑ b s = 0 ∑ c t = 0 ∑ d p ! q ! s ! t ! n ! [ p + q + s + t = n ] O ( n 2 log n ) O(n^2\log n) O ( n 2 log n )
[ARC160D] Mahjong
统计满足经过以下两种操作可以使得元素全为 0 0 0 n n n m m m A A A k k k k k k 1 1 1
数据范围:k , n ≤ 2000 , m ≤ 1 0 18 k, n \le 2000, m \le 10^{18} k , n ≤ 2 0 0 0 , m ≤ 1 0 1 8
有意思的计数题。注意到无解当且仅当 k ∤ m k\not\mid m k ∣ m B B B B B B 2 n − k + 1 2n-k+1 2 n − k + 1 B B B n n n B i = p B_i=p B i = p i i i p p p 1 1 1 B B B n − k + 1 n-k+1 n − k + 1 B i + n = p B_{i+n}=p B i + n = p i i i p p p B i < k ( n < i ≤ 2 n − k + 1 ) B_i < k(n < i \le 2n - k + 1) B i < k ( n < i ≤ 2 n − k + 1 ) B B B ∑ i = 1 2 n − k + 1 B i = m k \sum _{i=1}^{2n-k+1}B_i=\frac{m}{k} ∑ i = 1 2 n − k + 1 B i = k m B i B_i B i g i g_i g i i i i B i B_i B i g i = ( n − k + 1 i ) ( m k − i × k + 2 n − k 2 n − k ) g_i=\dbinom{n-k+1}{i}\dbinom{\frac{m}{k}-i\times k+2n-k}{2n-k} g i = ( i n − k + 1 ) ( 2 n − k k m − i × k + 2 n − k )
[ABC214G] Three Permutations
给定长度为 n n n p , q p, q p , q ∀ i ∈ [ 1 , n ] , r i ≠ p i , r i ≠ q i \forall i \in [1,n],r_i\not= p_i,r_i\not=q_i ∀ i ∈ [ 1 , n ] , r i = p i , r i = q i r r r
数据范围:n ≤ 3000 n \le 3000 n ≤ 3 0 0 0
考虑二项式反演,求出至少有 i i i h i h_i h i p i p_i p i q i q_i q i i i i i i i i i i d p i , j dp_{i, j} d p i , j i i i j j j i i i i i i d p n , m = ∑ i = 1 n i d p n − i , m − 1 dp_{n,m}=\sum_{i=1}^n idp_{n-i,m-1} d p n , m = ∑ i = 1 n i d p n − i , m − 1 f i , j f_{i,j} f i , j i i i j j j f n , m = ∑ i = 1 n i 2 f n − i , m − 1 f_{n, m} = \sum_{i=1}^n i^2 f_{n-i, m-1} f n , m = ∑ i = 1 n i 2 f n − i , m − 1 g i , j g_{i, j} g i , j i i i j j j g n , m = ∑ i = 1 v n g n − 1 , m f v n , i g_{n, m}=\sum_{i=1}^{v_{n}} g_{n-1, m}f_{v_n, i} g n , m = ∑ i = 1 v n g n − 1 , m f v n , i h i h_i h i g c n t , n − i g_{cnt, n-i} g c n t , n − i
随机立方体
有一个 n × m × l n\times m\times l n × m × l 1 ∼ n × m × l 1\sim n\times m\times l 1 ∼ n × m × l n × m × l n\times m\times l n × m × l n × m × l n\times m\times l n × m × l k k k
数据范围:n , m , l ≤ 5 × 1 0 6 , k ≤ 100 n, m, l \le 5\times 10^6, k\le 100 n , m , l ≤ 5 × 1 0 6 , k ≤ 1 0 0
看到恰好,直接二项式反演。我们只需要考虑至少有 k k k f ( k ) f(k) f ( k ) f ( i ) f(i) f ( i )
我们钦定完这 i i i ( n − i ) ( m − i ) ( l − i ) (n-i)(m-i)(l-i) ( n − i ) ( m − i ) ( l − i ) i i i
f i = ( n i ‾ m i ‾ l i ‾ ) ( ( n m l ) ( n − i ) ( m − i ) ( l − i ) ‾ ) g i f_i=(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}})\left ( (nml)^{\underline{(n-i)(m-i)(l-i)}}\right )g_i
f i = ( n i m i l i ) ( ( n m l ) ( n − i ) ( m − i ) ( l − i ) ) g i
第一项为选择这 i i i g i g_i g i
由于每个点可能会受到多个极大点的限制,因此我们需要从大到小来考虑填数,因为小的极大点的限制更强。我们结合下面这张图来推式子。
在图中,粉色部分为无限制区域,一半红的是放了关键点的区域,与关键点另一半相同颜色的区域是受该关键点控制的区域(这里为了方便,将关键点从左上到右下按从大到小排序)。这时我们可以计算一下:g ( 3 ) = 2 9 7 ‾ × 2 1 9 ‾ × 1 1 11 ‾ g(3)=29^{\underline{7}}\times 21^{\underline{9}}\times 11^{\underline{11}} g ( 3 ) = 2 9 7 × 2 1 9 × 1 1 1 1
因此我们可以得到 g i g_i g i
设 h ( x ) = ( n − x ) ( m − x ) ( l − x ) h(x)=(n-x)(m-x)(l-x) h ( x ) = ( n − x ) ( m − x ) ( l − x )
g i = ∏ j = 1 i ( h ( 0 ) − h ( j ) − 1 ) h ( j − 1 ) − h ( j ) − 1 ‾ = ∏ j = 1 i ( h ( 0 ) − h ( j ) − 1 ) ! ( h ( 0 ) − h ( j − 1 ) ) ! = ( h ( 0 ) − h ( i ) − 1 ) ! ∏ j = 1 i − 1 1 ( h ( 0 ) − h ( j ) ) ! \begin{aligned}
g_i&=\prod_{j=1}^{i}(h(0)-h(j)-1)^{\underline{h(j-1)-h(j)-1}}\\
&=\prod _{j=1}^i \frac{(h(0)-h(j)-1)!}{(h(0)-h(j-1))!} \\
&=(h(0)-h(i)-1)!\prod_{j=1}^{i-1} \frac{1}{(h(0)-h(j))!}
\end{aligned}
g i = j = 1 ∏ i ( h ( 0 ) − h ( j ) − 1 ) h ( j − 1 ) − h ( j ) − 1 = j = 1 ∏ i ( h ( 0 ) − h ( j − 1 ) ) ! ( h ( 0 ) − h ( j ) − 1 ) ! = ( h ( 0 ) − h ( i ) − 1 ) ! j = 1 ∏ i − 1 ( h ( 0 ) − h ( j ) ) ! 1
再带回 f i f_i f i
f i = ( n i ‾ m i ‾ l i ‾ ) ( ( n m l ) ( n − i ) ( m − i ) ( l − i ) ‾ ) g i = ( n i ‾ m i ‾ l i ‾ ) ( ( n m l ) ( n − i ) ( m − i ) ( l − i ) ‾ ) ( h ( 0 ) − h ( i ) − 1 ) ! ∏ j = 1 i − 1 1 ( h ( 0 ) − h ( j ) ) ! = ( n i ‾ m i ‾ l i ‾ ) ( n m l ) ! ( n m l − h ( i ) ) ( n m l − h ( i ) − 1 ) ! ∏ j = 1 i − 1 1 n m l − h ( j ) = ( n i ‾ m i ‾ l i ‾ ) ( n m l ) ! ∏ j = 1 i 1 n m l − h ( j ) \begin{aligned}
f_i & = (n^{\underline{i}}m^{\underline{i}}l^{\underline{i}})\left ( (nml)^{\underline{(n-i)(m-i)(l-i)}}\right )g_i\\
&=(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}})\left ( (nml)^{\underline{(n-i)(m-i)(l-i)}}\right )(h(0)-h(i)-1)!\prod_{j=1}^{i-1} \frac{1}{(h(0)-h(j))!}\\
&=(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}})\frac{(nml)!}{(nml-h(i))}(nml-h(i)-1)!\prod_{j=1}^{i-1}\frac{1}{nml-h(j)} \\
&=(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}})(nml)!\prod_{j=1}^{i}\frac{1}{nml-h(j)} \\
\end{aligned}
f i = ( n i m i l i ) ( ( n m l ) ( n − i ) ( m − i ) ( l − i ) ) g i = ( n i m i l i ) ( ( n m l ) ( n − i ) ( m − i ) ( l − i ) ) ( h ( 0 ) − h ( i ) − 1 ) ! j = 1 ∏ i − 1 ( h ( 0 ) − h ( j ) ) ! 1 = ( n i m i l i ) ( n m l − h ( i ) ) ( n m l ) ! ( n m l − h ( i ) − 1 ) ! j = 1 ∏ i − 1 n m l − h ( j ) 1 = ( n i m i l i ) ( n m l ) ! j = 1 ∏ i n m l − h ( j ) 1
由于最终还要除掉 ( n m l ) ! (nml)! ( n m l ) !
f ( i ) = ( n i ‾ m i ‾ l i ‾ ) ∏ j = 1 i 1 n m l − h ( j ) a n s = ∑ i = k ( − 1 ) i − k ( i k ) f ( i ) \begin{aligned}
f(i)&=(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}})\prod_{j=1}^{i}\frac{1}{nml-h(j)} \\
ans&=\sum \limits _{i=k}(-1)^{i-k}\dbinom{i}{k}f(i)
\end{aligned}
f ( i ) a n s = ( n i m i l i ) j = 1 ∏ i n m l − h ( j ) 1 = i = k ∑ ( − 1 ) i − k ( k i ) f ( i )
Ban Permutation
问长度为 n n n ∀ i , ∣ i − p i ∣ ≥ X \forall i, |i-p_i|\ge X ∀ i , ∣ i − p i ∣ ≥ X
数据范围:n ≤ 100 , X ≤ 5 n\le 100, X \le 5 n ≤ 1 0 0 , X ≤ 5
我们先用二项式反演将题目的限制变为 ∣ i − p i ∣ < X |i-p_i|<X ∣ i − p i ∣ < X i i i
我们设 g i , j , s g_{i, j, s} g i , j , s i i i j j j [ i − X + 1 , i + X − 1 ] [i-X+1, i+X-1] [ i − X + 1 , i + X − 1 ] s s s
g i , j , T = g i − 1 , j , s + ∑ g i − 1 , j − 1 , s ′ g_{i, j, T}=g_{i-1,j,s}+\sum g_{i-1, j-1, s'}
g i , j , T = g i − 1 , j , s + ∑ g i − 1 , j − 1 , s ′
这样就能求出钦定 i i i
时间复杂度 O ( 4 X n 2 ) O(4^Xn^2) O ( 4 X n 2 )
Lamps and Buttons
有 n n n m m m p p p i i i i i i i i i p i p_i p i p p p p p p
数据范围:n ≤ 1 0 7 , m ≤ 5000 n \le 10^7, m\le 5000 n ≤ 1 0 7 , m ≤ 5 0 0 0
我们把 i i i p i p_i p i p p p
我们枚举第一个自环的位置 i i i x x x n − m n-m n − m i − x i-x i − x a = i − x − 1 , b = n − m , c = m − i a=i-x-1, b = n-m, c = m-i a = i − x − 1 , b = n − m , c = m − i
1 × 2 × ⋯ × a × a × ( a + 1 ) × ⋯ × ( a + b − 1 ) × ( a + b + 1 ) × ⋯ ( a + b + c ) = a ( a + b + c ) ( a + b ) 1\times 2\times \cdots \times a\times a\times (a+1)\times \cdots \times (a+b-1)\times (a+b+1)\times \cdots(a+b+c)=\frac{a(a+b+c)}{(a+b)}
1 × 2 × ⋯ × a × a × ( a + 1 ) × ⋯ × ( a + b − 1 ) × ( a + b + 1 ) × ⋯ ( a + b + c ) = ( a + b ) a ( a + b + c )
总时间复杂度 O ( n + m 2 ) O(n+m^2) O ( n + m 2 )
成绩比较
G 系共有 n n n m m m n n n 0 0 0 n − 1 n-1 n − 1 0 0 0 m m m 0 0 0 m − 1 m-1 m − 1 1 1 1 u i u_i u i
如果在每门课上 A 获得的成绩均小于等于 B 获得的成绩,则称 A 被 B 碾压。在 B 神的说法中,G 系共有 k k k n − k − 1 n-k-1 n − k − 1 r i r_i r i
求出全系所有同学每门必修课得分的情况数,使其既能满足 B 神的说法,也能符合 D 神查到的排名。这里两种情况不同当且仅当有任意一位同学在任意一门课上获得的分数不同。
数据范围:n , m , r i ≤ 100 , u i ≤ 1 0 9 n, m, r_i\le 100, u_i\le 10^9 n , m , r i ≤ 1 0 0 , u i ≤ 1 0 9
首先我们发现恰好 k k k
我们设 g i g_i g i i i i
a n s = ∑ i = k n − 1 ( i k ) ( − 1 ) i − k g i ans=\sum\limits_{i=k}^{n-1}\dbinom{i}{k}(-1)^{i-k}g_i
a n s = i = k ∑ n − 1 ( k i ) ( − 1 ) i − k g i
我们现在就考虑如何求出 g i g_i g i i i i n − 1 − i n-1-i n − 1 − i n − r i − i n-r_i-i n − r i − i
因此我们最终出来的式子是:
g i = ( n − 1 i ) ∏ j = 1 m ( n − i − 1 n − r j − i ) ∑ k = 1 u j k n − r j ( u j − k ) r j − 1 g_i=\dbinom{n-1}{i}\prod_{j=1}^m\dbinom{n-i-1}{n-r_j-i}\sum\limits_{k=1}^{u_j} k^{n-r_j}(u_j-k)^{r_j-1}
g i = ( i n − 1 ) j = 1 ∏ m ( n − r j − i n − i − 1 ) k = 1 ∑ u j k n − r j ( u j − k ) r j − 1
然后我们发现最后的 ∑ \sum ∑ u u u
g i = ( n − 1 i ) ∏ j = 1 m ( n − i − 1 n − r j − i ) ∑ k = 1 u j k n − r j ( u j − k ) r j − 1 = ( n − 1 i ) ∏ j = 1 m ( n − i − 1 n − r j − i ) ∑ k = 1 u j k n − r j ∑ l = 0 r j − 1 ( r j − 1 l ) ( − k ) l u j r j − 1 − l = ( n − 1 i ) ∏ j = 1 m ( n − i − 1 n − r j − i ) ∑ l = 0 r j − 1 ( r j − 1 l ) u j r j − 1 − l ( − 1 ) l ∑ k = 1 u j k n − r j + l \begin{aligned}
g_i&=\dbinom{n-1}{i}\prod_{j=1}^m\dbinom{n-i-1}{n-r_j-i}\sum\limits_{k=1}^{u_j} k^{n-r_j}(u_j-k)^{r_j-1}\\
&=\dbinom{n-1}{i}\prod_{j=1}^m\dbinom{n-i-1}{n-r_j-i}\sum\limits_{k=1}^{u_j}k^{n-r_j}\sum\limits_{l=0}^{r_j-1}\dbinom{r_j-1}{l}(-k)^l u_j^{r_j-1-l}\\
&=\dbinom{n-1}{i}\prod_{j=1}^m\dbinom{n-i-1}{n-r_j-i}\sum\limits_{l=0}^{r_j-1}\dbinom{r_j-1}{l}u_j^{r_j-1-l}(-1)^l\sum\limits_{k=1}^{u_j}k^{n-r_j+l}
\end{aligned}
g i = ( i n − 1 ) j = 1 ∏ m ( n − r j − i n − i − 1 ) k = 1 ∑ u j k n − r j ( u j − k ) r j − 1 = ( i n − 1 ) j = 1 ∏ m ( n − r j − i n − i − 1 ) k = 1 ∑ u j k n − r j l = 0 ∑ r j − 1 ( l r j − 1 ) ( − k ) l u j r j − 1 − l = ( i n − 1 ) j = 1 ∏ m ( n − r j − i n − i − 1 ) l = 0 ∑ r j − 1 ( l r j − 1 ) u j r j − 1 − l ( − 1 ) l k = 1 ∑ u j k n − r j + l
我们发现最后的 ∑ k = 1 u j k n − r j + l \sum\limits_{k=1}^{u_j}k^{n-r_j+l} k = 1 ∑ u j k n − r j + l O ( n ) O(n) O ( n )
时间复杂度 O ( n 3 ) O(n^3) O ( n 3 )
Natasha, Sasha and the Prefix Sums
一个长度为 n + m n+m n + m n n n 1 1 1 m m m − 1 -1 − 1 a a a max { 0 , max 1 ≤ i ≤ n + m ∑ j = 1 i a j } \max\{ 0,\max\limits_{1\le i\le n+m}\sum\limits_{j=1}^ia_j \} max { 0 , 1 ≤ i ≤ n + m max j = 1 ∑ i a j }
求出对于全部可能的序列,它们的最大前缀和之和是多少。
0 ≤ n , m ≤ 2000 0\le n,m \le 2000 0 ≤ n , m ≤ 2 0 0 0
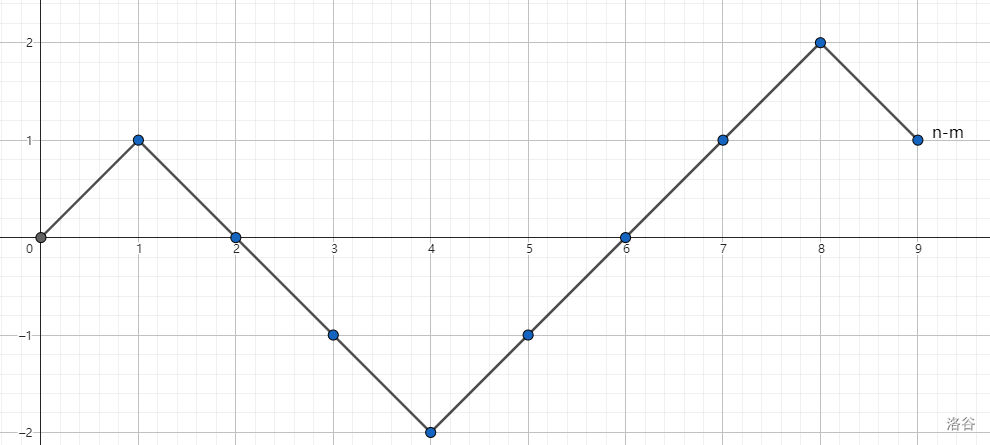
我们可以把放入 1 1 1 − 1 -1 − 1 1 1 1 − 1 -1 − 1 ( m , n ) (m, n) ( m , n )
如果一条折线能顶到的最高的直线为 y = x + k y=x+k y = x + k k k k
这样的一条路径对应的序列就是 -1 -1 1 1 1 -1 1 -1 -1 -1 -1,显然它的最大前缀和就是 1 1 1 y = x + 1 y=x+1 y = x + 1
因此我们现在要计算的就是对于每一条 y = x + k y=x+k y = x + k k k k
我们可以考虑容斥,我们用经过 y = x + k y=x+k y = x + k y = x + k + 1 y=x+k+1 y = x + k + 1 y = x + k y=x+k y = x + k y = x + k y=x+k y = x + k ( n + m n − k ) \dbinom{n+m}{n-k} ( n − k n + m )
这样枚举每一条 y = x + k y=x+k y = x + k
时间复杂度 O ( n ) O(n) O ( n )
博弈论与概率统计
Alice 和 Bob 在玩一个双人游戏。每一轮中,Alice 有 p p p 1 − p 1-p 1 − p
双方初始时各有 0 0 0 0 0 0 n , m n, m n , m n + m n+m n + m n n n
数据范围:n + m , q ≤ 2.5 × 1 0 5 n+m, q\le 2.5\times 10^5 n + m , q ≤ 2 . 5 × 1 0 5
首先题目中的 p p p ( n + m n ) \dbinom{n+m}{n} ( n n + m )
我们考虑总得分如何计算。我们先假设没有减到 0 0 0
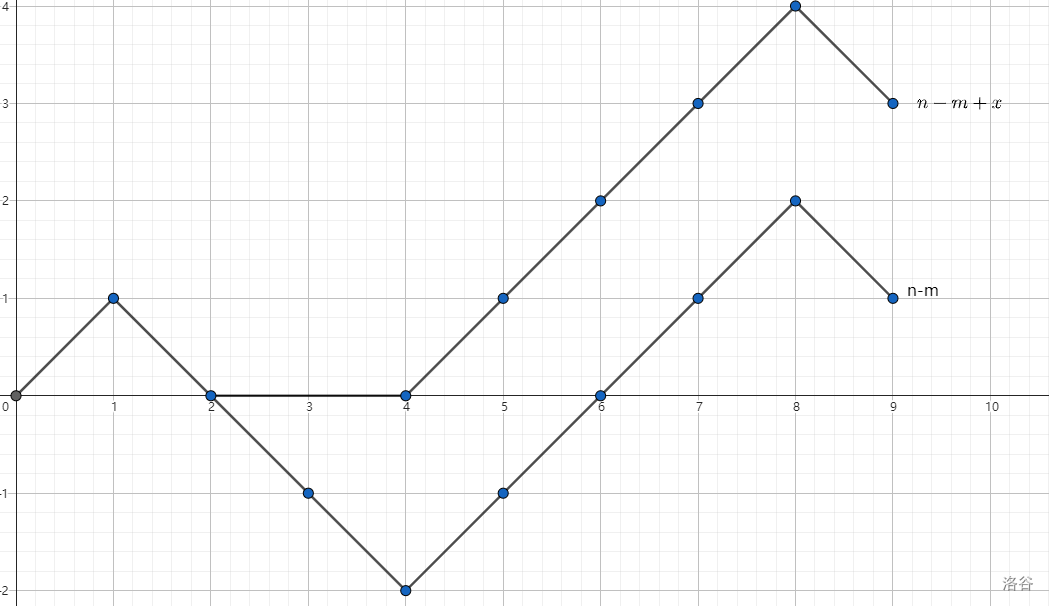
但是我们有了保护机制,因此折线应该是这样的:
最终得分会增加遇到的最低的线,转化到上面的那个网格图中即为:一条折线与 y = x + b y=x+b y = x + b b b b y = x + b y=x+b y = x + b y = x + b − 1 y=x+b-1 y = x + b − 1 y = x + b y=x+b y = x + b y = x + b y=x+b y = x + b ( n + m n + b − 1 ) − ( n + m n + b ) \dbinom{n+m}{n+b-1} - \dbinom{n+m}{n+b} ( n + b − 1 n + m ) − ( n + b n + m )
这样我们就能列出下面的式子:
a n s = ∑ i = 0 m ( ( n + m n + i ) − ( n + m n + i + 1 ) ) ( n − m + i ) = ( n − m ) ( n + m n ) + ∑ i = 0 m − 1 ( n + m i ) \begin{aligned}
ans & = \sum \limits_{i = 0}^{m} \left ( \dbinom{n+m}{n+i}-\dbinom{n+m}{n+i+1} \right )(n-m+i)\\
&=(n-m)\dbinom{n+m}{n}+\sum \limits_{i=0}^{m-1}\dbinom{n+m}{i}
\end{aligned}
a n s = i = 0 ∑ m ( ( n + i n + m ) − ( n + i + 1 n + m ) ) ( n − m + i ) = ( n − m ) ( n n + m ) + i = 0 ∑ m − 1 ( i n + m )
这里我们只考虑了 n ≥ m n\ge m n ≥ m n < m n<m n < m ∑ i = 0 m − 1 ( n + m i ) \sum \limits_{i=0}^{m-1}\dbinom{n+m}{i} i = 0 ∑ m − 1 ( i n + m )
我们这里可以考虑莫队,我们设 f ( l , r ) = ∑ i = 0 r ( l i ) f(l, r)=\sum \limits_{i=0}^{r}\dbinom{l}{i} f ( l , r ) = i = 0 ∑ r ( i l ) l , r l, r l , r O ( 1 ) O(1) O ( 1 )
因此时间复杂度 O ( n n ) O(n\sqrt n) O ( n n )
Team Work
给定 n , k n,k n , k ∑ i = 1 n ( n i ) × i k \sum_{i=1}^n\binom n i \times i^k ∑ i = 1 n ( i n ) × i k
数据范围:1 ≤ k ≤ 5000 , 1 ≤ n ≤ 1 0 9 1 \leq k \leq 5000,1 \leq n \leq 10^9 1 ≤ k ≤ 5 0 0 0 , 1 ≤ n ≤ 1 0 9
∑ i = 1 n ( n i ) i k = ∑ i = 0 n ( n i ) ∑ j = 0 k { k j } ( i j ) j ! = ∑ j = 0 k { k j } j ! ∑ i = 0 n ( n i ) ( i j ) = ∑ j = 0 k { k j } j ! ∑ i = 0 n ( n j ) ( n − j i − j ) = ∑ j = 0 k { k j } j ! ( n j ) ∑ i = 0 n ( n − j i − j ) = ∑ j = 0 k { k j } n ! ( n − j ) ! 2 n − j \begin{aligned}
\sum \limits_{i=1}^n \dbinom{n}{i}i^k&=\sum \limits _{i=0}^n\dbinom{n}{i}\sum \limits _{j=0}^k {k\brace j}\dbinom{i}{j}j!\\
&=\sum \limits _{j=0}^k{k \brace j}j!\sum \limits_{i=0}^n\dbinom{n}{i}\dbinom{i}{j}\\
&= \sum \limits _{j=0}^k{k\brace j}j!\sum \limits _{i=0}^n\dbinom{n}{j}\dbinom{n-j}{i-j}\\
&=\sum \limits _{j=0}^k{k\brace j}j!\dbinom{n}{j}\sum \limits_{i=0}^n\dbinom{n-j}{i-j}\\
&=\sum \limits _{j=0}^k {k\brace j} \frac{n!}{(n-j)!}2^{n-j}
\end{aligned}
i = 1 ∑ n ( i n ) i k = i = 0 ∑ n ( i n ) j = 0 ∑ k { j k } ( j i ) j ! = j = 0 ∑ k { j k } j ! i = 0 ∑ n ( i n ) ( j i ) = j = 0 ∑ k { j k } j ! i = 0 ∑ n ( j n ) ( i − j n − j ) = j = 0 ∑ k { j k } j ! ( j n ) i = 0 ∑ n ( i − j n − j ) = j = 0 ∑ k { j k } ( n − j ) ! n ! 2 n − j
直接 O ( n 2 ) O(n^2) O ( n 2 )
[HEOI2016/TJOI2016]求和
求 ∑ i = 0 n ∑ j = 0 i { i j } 2 j × j ! \sum \limits _{i=0}^n\sum \limits _{j=0}^i{i\brace j}2^j\times j! i = 0 ∑ n j = 0 ∑ i { j i } 2 j × j !
数据范围:n ≤ 1 0 5 n \le 10^5 n ≤ 1 0 5
∑ i = 0 n ∑ j = 0 i { i j } 2 j × j ! = ∑ j = 0 n 2 j j ! ∑ i = 0 n { i j } = ∑ j = 0 n 2 j j ! ∑ i = 0 n ∑ k = 0 j ( − 1 ) j − k k i k ! ( j − k ) ! = ∑ j = 0 n 2 j j ! ∑ k = 0 j ( − 1 ) j − k k ! ( j − k ) ! ∑ i = 0 n k i = ∑ j = 0 n 2 j j ! ∑ k = 0 j ( − 1 ) j − k ( j − k ) ! ( k n + 1 − 1 ) ( k ! ) ( k − 1 ) \begin{aligned}
\sum \limits _{i = 0}^n\sum \limits _{j = 0}^i{i\brace j}2^j\times j!&=\sum \limits _{j=0}^n2^jj!\sum \limits _{i=0}^n{i\brace j}\\
&=\sum \limits _{j=0}^n2^jj!\sum \limits _{i=0}^n\sum \limits _{k=0}^j\frac{(-1)^{j-k}k^i}{k!(j-k)!}\\
&=\sum \limits _{j=0}^n2^jj!\sum \limits _{k=0}^j\frac{(-1)^{j-k}}{k!(j-k)!}\sum \limits _{i=0}^n k^i\\
&= \sum \limits _{j=0}^n2^jj!\sum \limits _{k=0}^j\frac{(-1)^{j-k}}{(j-k)!}\frac{(k^{n+1}-1)}{(k!)(k-1)}
\end{aligned}
i = 0 ∑ n j = 0 ∑ i { j i } 2 j × j ! = j = 0 ∑ n 2 j j ! i = 0 ∑ n { j i } = j = 0 ∑ n 2 j j ! i = 0 ∑ n k = 0 ∑ j k ! ( j − k ) ! ( − 1 ) j − k k i = j = 0 ∑ n 2 j j ! k = 0 ∑ j k ! ( j − k ) ! ( − 1 ) j − k i = 0 ∑ n k i = j = 0 ∑ n 2 j j ! k = 0 ∑ j ( j − k ) ! ( − 1 ) j − k ( k ! ) ( k − 1 ) ( k n + 1 − 1 )
推出卷积形式直接 NTT 即可。
[国家集训队] Crash 的文明世界
给定一棵树,对于每个点 i i i ∑ j = 1 n d i s t i , j k \sum \limits _{j=1}^ndist_{i,j}^k j = 1 ∑ n d i s t i , j k
数据范围:n ≤ 50000 , k ≤ 150 n \le 50000, k \le 150 n ≤ 5 0 0 0 0 , k ≤ 1 5 0
∑ i = 1 n d i s t u , i k = ∑ i = 1 n ∑ j = 0 k { k j } j ! ( d i s t u , i j ) = ∑ j = 0 k { k j } j ! ∑ i = 1 n ( d i s t u , i j ) \begin{aligned}
\sum \limits _{i = 1}^ndist_{u, i}^k &= \sum \limits _{i=1}^n\sum \limits _{j=0}^k{k\brace j}j!\dbinom{dist_{u,i}}{j}\\
&=\sum \limits _{j=0}^k {k\brace j}j!\sum \limits _{i=1}^n\dbinom{dist_{u,i}}{j}\\
\end{aligned}
i = 1 ∑ n d i s t u , i k = i = 1 ∑ n j = 0 ∑ k { j k } j ! ( j d i s t u , i ) = j = 0 ∑ k { j k } j ! i = 1 ∑ n ( j d i s t u , i )
因此我们只需要求出对于每个点的 ∑ i = 1 n ( d i s t u , i j ) \sum \limits _{i=1}^n\dbinom{dist_{u,i}}{j} i = 1 ∑ n ( j d i s t u , i ) a n s u , j ans_{u, j} a n s u , j u u u ( d i s t u , i j ) \dbinom{dist_{u,i}}{j} ( j d i s t u , i ) ( n m ) = ( n − 1 m ) + ( n − 1 m − 1 ) \dbinom{n}{m}=\dbinom{n-1}{m}+\dbinom{n-1}{m-1} ( m n ) = ( m n − 1 ) + ( m − 1 n − 1 ) a n s u , j = ∑ v ∈ s o n u a n s v , j + a n s v , j − 1 ans_{u,j}=\sum \limits _{v\in son_u}ans_{v, j}+ans_{v, j-1} a n s u , j = v ∈ s o n u ∑ a n s v , j + a n s v , j − 1
CF1278F Cards
有 m m m n n n x x x x k x^k x k
数据范围:n , m < 998244353 , k ≤ 5000 n, m< 998244353, k \le 5000 n , m < 9 9 8 2 4 4 3 5 3 , k ≤ 5 0 0 0
a n s = ∑ i = 0 n ( n i ) ( 1 m ) i ( m − 1 m ) n − i i k = ∑ i = 0 n ( n i ) ( 1 m ) i ( m − 1 m ) n − i ∑ j = 0 k ( i j ) j ! { k j } = 1 m n ∑ j = 0 k { k j } j ! ∑ i = 0 n ( m − 1 ) n − i ( n i ) ( i j ) = 1 m n ∑ j = 0 k { k j } j ! ∑ i = 0 n ( m − 1 ) n − i ( n j ) ( n − j i − j ) = 1 m n ∑ j = 0 k { k j } j ! ( n j ) ∑ i = 0 n − j ( n − j i ) ( m − 1 ) n − i − j × 1 i = 1 m n ∑ j = 0 k { k j } j ! ( n j ) m n − j = ∑ j = 0 k { k j } n ! ( n − j ) ! × 1 m j \begin{aligned}ans &= \sum \limits_{i=0}^n\dbinom{n}{i}(\frac{1}{m})^i(\frac{m-1}{m})^{n-i}i^k\\ &=\sum\limits_{i=0}^n\dbinom{n}{i}(\frac{1}{m})^i(\frac{m-1}{m})^{n-i}\sum\limits _{j=0}^k\dbinom{i}{j}j!{k\brace j}\\&=\frac{1}{m^n}\sum \limits_{j=0}^k{k\brace j}j!\sum \limits _{i=0}^n(m-1)^{n-i}\dbinom{n}{i}\dbinom{i}{j}\\&= \frac{1}{m^n}\sum \limits_{j=0}^k{k\brace j}j!\sum \limits _{i=0}^n(m-1)^{n-i}\dbinom{n}{j}\dbinom{n-j}{i-j}\\&=\frac{1}{m^n}\sum \limits_{j=0}^k{k\brace j}j!\dbinom{n}{j}\sum\limits_{i=0}^{n-j}\dbinom{n-j}{i}(m-1)^{n-i-j}\times 1^{i}\\&=\frac{1}{m^n}\sum \limits_{j=0}^k{k \brace j}j!\dbinom{n}{j}m^{n-j}\\&= \sum \limits_{j=0}^k{k \brace j}\frac{n!}{(n-j)!} \times \frac{1}{m^j} \end{aligned}
a n s = i = 0 ∑ n ( i n ) ( m 1 ) i ( m m − 1 ) n − i i k = i = 0 ∑ n ( i n ) ( m 1 ) i ( m m − 1 ) n − i j = 0 ∑ k ( j i ) j ! { j k } = m n 1 j = 0 ∑ k { j k } j ! i = 0 ∑ n ( m − 1 ) n − i ( i n ) ( j i ) = m n 1 j = 0 ∑ k { j k } j ! i = 0 ∑ n ( m − 1 ) n − i ( j n ) ( i − j n − j ) = m n 1 j = 0 ∑ k { j k } j ! ( j n ) i = 0 ∑ n − j ( i n − j ) ( m − 1 ) n − i − j × 1 i = m n 1 j = 0 ∑ k { j k } j ! ( j n ) m n − j = j = 0 ∑ k { j k } ( n − j ) ! n ! × m j 1
O ( n 2 ) O(n^2) O ( n 2 )
Partitions
有 n n n w i w_i w i W ( S ) = ∣ S ∣ ∑ w i W(S)=|S|\sum w_i W ( S ) = ∣ S ∣ ∑ w i n n n k k k
数据范围:n , k ≤ 2 × 1 0 5 n, k \le 2\times 10^5 n , k ≤ 2 × 1 0 5
易知每个物品在所有划分方案中贡献的次数是相同的,记为 c n t cnt c n t
c n t = ∑ s = 1 n ( s × ( n − 1 s − 1 ) × { n − s k − 1 } ) = ∑ s = 1 n s ( n − 1 s − 1 ) ∑ i = 0 k − 1 ( − 1 ) i ( k − 1 − i ) n − s i ! ( k − 1 − i ) ! = ∑ i = 1 k − 1 ( − 1 ) i i ! ( k − 1 − i ) ! ∑ s = 1 n s ( n − 1 s − 1 ) ( k − 1 − i ) n − s \begin{aligned}
cnt &= \sum\limits_{s=1}^n(s\times \dbinom{n-1}{s-1}\times {n-s\brace k-1})\\
&=\sum \limits_{s=1}^ns\dbinom{n-1}{s-1}\sum \limits_{i=0}^{k-1}\frac{(-1)^i(k-1-i)^{n-s}}{i!(k-1-i)!}\\
&=\sum\limits _{i=1}^{k-1}\frac{(-1)^i}{i!(k-1-i)!}\sum \limits _{s=1}^ns\dbinom{n-1}{s-1}(k-1-i)^{n-s}
\end{aligned}
c n t = s = 1 ∑ n ( s × ( s − 1 n − 1 ) × { k − 1 n − s } ) = s = 1 ∑ n s ( s − 1 n − 1 ) i = 0 ∑ k − 1 i ! ( k − 1 − i ) ! ( − 1 ) i ( k − 1 − i ) n − s = i = 1 ∑ k − 1 i ! ( k − 1 − i ) ! ( − 1 ) i s = 1 ∑ n s ( s − 1 n − 1 ) ( k − 1 − i ) n − s
我们再单独考虑后面的和式。
有一个公式 m ( n m ) = n ( n − 1 m − 1 ) m\dbinom{n}{m}=n\dbinom{n-1}{m-1} m ( m n ) = n ( m − 1 n − 1 )
t m p = ∑ s = 1 n ( n − 1 s − 1 ) ( k − 1 − i ) n − s + ∑ s = 1 n ( s − 1 ) ( n − 1 s − 1 ) ( k − 1 − i ) n − s = ∑ s = 1 n ( n − 1 s − 1 ) ( k − 1 − i ) n − s + ( n − 1 ) ∑ s = 1 n ( n − 2 s − 2 ) ( k − 1 − i ) n − s \begin{aligned}
tmp&=\sum \limits_{s=1}^n\dbinom{n-1}{s-1}(k-1-i)^{n-s}+\sum \limits _{s=1}^n(s-1)\dbinom{n-1}{s-1}(k-1-i)^{n-s}\\
&=\sum \limits_{s=1}^n\dbinom{n-1}{s-1}(k-1-i)^{n-s}+(n-1)\sum \limits _{s=1}^n\dbinom{n-2}{s-2}(k-1-i)^{n-s}\\
\end{aligned}
t m p = s = 1 ∑ n ( s − 1 n − 1 ) ( k − 1 − i ) n − s + s = 1 ∑ n ( s − 1 ) ( s − 1 n − 1 ) ( k − 1 − i ) n − s = s = 1 ∑ n ( s − 1 n − 1 ) ( k − 1 − i ) n − s + ( n − 1 ) s = 1 ∑ n ( s − 2 n − 2 ) ( k − 1 − i ) n − s
然后二项式定理即可。
t m p = ( k − i ) n − 1 + ( n − 1 ) ( k − i ) n − 2 = ( k − i ) n − 2 ( k − i + n − 1 ) \begin{aligned}
tmp&=(k-i)^{n-1}+(n-1)(k-i)^{n-2}\\
&=(k-i)^{n-2}(k-i+n-1)
\end{aligned}
t m p = ( k − i ) n − 1 + ( n − 1 ) ( k − i ) n − 2 = ( k − i ) n − 2 ( k − i + n − 1 )
因此最终答案为 ∑ i = 1 k − 1 ( − 1 ) i ( k − i ) n − 2 ( k − i + n − 1 ) i ! ( k − 1 − i ) ! \sum\limits _{i=1}^{k-1}\frac{(-1)^i(k-i)^{n-2}(k-i+n-1)}{i!(k-1-i)!} i = 1 ∑ k − 1 i ! ( k − 1 − i ) ! ( − 1 ) i ( k − i ) n − 2 ( k − i + n − 1 )
[省选联考 2020 A 卷] 组合数问题
给定一个 m m m f ( x ) = a 0 + a 1 x + ⋯ + a m x m f(x)=a_0+a_1x+\cdots +a_mx^m f ( x ) = a 0 + a 1 x + ⋯ + a m x m ∑ k = 0 n f ( k ) × x k × ( n k ) \sum \limits_{k=0}^nf(k)\times x^k\times \dbinom{n}{k} k = 0 ∑ n f ( k ) × x k × ( k n )
数据范围:n ≤ 1 0 9 , m ≤ 1000 n \le 10^9, m \le 1000 n ≤ 1 0 9 , m ≤ 1 0 0 0
本题要用新科技:下降幂。本来不想写这题的发现有不会的新科技才写的
我们先把 f ( x ) f(x) f ( x ) f ( x ) = b 0 + b 1 x + ⋯ b m x m ‾ f(x)=b_0+b_1x+\cdots b_m x^{\underline{m}} f ( x ) = b 0 + b 1 x + ⋯ b m x m
∑ i = 0 n f ( i ) x i ( n i ) = ∑ i = 0 n ∑ j = 0 m b j × i j ‾ ( n i ) x i = ∑ i = 0 n ∑ j = 0 m b j × n j ‾ ( n − j i − j ) x i = ∑ i = 0 n x i ∑ j = 0 m b j × n j ‾ ( n − j i − j ) = ∑ j = 0 m b j n j ‾ ∑ i = 0 n ( n − j i − j ) x i = ∑ j = 0 m b j n j ‾ ∑ i = 0 n − j ( n − j i ) x i + j = ∑ j = 0 m b j n j ‾ x j ∑ i = 0 n − j ( n − j i ) x i = ∑ j = 0 m b j n j ‾ x j ( x + 1 ) n − j \begin{aligned}
\sum \limits _{i = 0}^nf(i)x^i\dbinom{n}{i} &=\sum \limits_{i=0}^n\sum \limits _{j=0}^mb_j\times i^{\underline{j}}\dbinom{n}{i}x^i\\
&= \sum \limits_{i=0}^n\sum \limits _{j=0}^mb_j\times n^{\underline{j}}\dbinom{n-j}{i-j}x^i\\
&=\sum \limits_{i=0}^nx^i\sum \limits _{j=0}^mb_j\times n^{\underline{j}}\dbinom{n-j}{i-j}\\
&=\sum \limits_{j=0}^mb_jn^{\underline{j}}\sum \limits_{i=0}^n\dbinom{n-j}{i-j}x^i\\
&= \sum \limits_{j=0}^mb_jn^{\underline{j}}\sum \limits_{i=0}^{n-j}\dbinom{n-j}{i}x^{i+j}\\
&=\sum \limits_{j=0}^mb_jn^{\underline{j}}x^j\sum \limits_{i=0}^{n-j}\dbinom{n-j}{i}x^{i}\\
&=\sum \limits_{j=0}^mb_jn^{\underline{j}}x^j(x+1)^{n-j}
\end{aligned}
i = 0 ∑ n f ( i ) x i ( i n ) = i = 0 ∑ n j = 0 ∑ m b j × i j ( i n ) x i = i = 0 ∑ n j = 0 ∑ m b j × n j ( i − j n − j ) x i = i = 0 ∑ n x i j = 0 ∑ m b j × n j ( i − j n − j ) = j = 0 ∑ m b j n j i = 0 ∑ n ( i − j n − j ) x i = j = 0 ∑ m b j n j i = 0 ∑ n − j ( i n − j ) x i + j = j = 0 ∑ m b j n j x j i = 0 ∑ n − j ( i n − j ) x i = j = 0 ∑ m b j n j x j ( x + 1 ) n − j
再回顾一开始普通幂转下降幂的式子,则有
∑ i = 0 m a i x i = ∑ i = 0 m a i ∑ j = 0 i { i j } x j ‾ = ∑ i = 0 m x i ‾ ∑ j = i m { j i } a j \sum\limits_{i=0}^ma_ix^i=\sum \limits_{i=0}^ma_i\sum \limits _{j=0}^i{i\brace j}x^{\underline{j}}=\sum \limits_{i=0}^mx^{\underline{i}}\sum \limits _{j=i}^m{j\brace i}a_j
i = 0 ∑ m a i x i = i = 0 ∑ m a i j = 0 ∑ i { j i } x j = i = 0 ∑ m x i j = i ∑ m { i j } a j
因此 b j = ∑ j = i m { j i } a j b_j=\sum \limits _{j=i}^m{j\brace i}a_j b j = j = i ∑ m { i j } a j O ( n 2 ) O(n^2) O ( n 2 )
组合数学博客也肝了一段时间了,从开始做到肝完博客也花了十天左右,以后可能还会加点有意思的组合数学题(也感觉自己数数能力好了点)。