学习笔记字符串

PAM（回文自动机）

PAM

回文树（又称回文自动机 PAM\texttt{PAM}），是一种可以高效解决大部分回文串问题的算法，在大部分情况下可以替代马拉车（当然模板题好像都替代不了），是一种不错的算法。

结构

trie

类似于其他的自动机（AC\texttt {AC} 自动机、SAM\texttt{SAM}），PAM\texttt{PAM} 也有一颗 trie\texttt{trie} 树以及相应的 fail\texttt{fail} 指针。但是不太相同的是，在 PAM\texttt{PAM} 中，有两棵树。

为什么呢？因为回文串分为奇回文串和偶回文串，奇回文串当然可以直接插入，但是偶回文串就出现了问题。我们当然可以用类似马拉车的方法，添加不存在的字符来使它变成奇回文串，但是这样太麻烦了。于是我们可以建立两棵树，一颗奇树，一颗偶树，奇树的儿子都代表奇回文串，偶树的儿子都代表偶回文串。

下图是字符串为 abaaabacca\texttt{abaaabacca} 的回文树。

手绘不行请见谅

在这个字符串中，出现了以下这些回文串：

a,b,c,aba,aaa,cc,acca,baaab,abaaaba\texttt{a},\texttt{b},\texttt{c},\texttt{aba},\texttt{aaa},\texttt{cc},\texttt{acca},\texttt{baaab},\texttt{abaaaba}

我们可以注意到，在这个 trie 树上，一条转移边代表的是在字符串两边加上同一个字符，这也符合回文串的定义。

fail 指针

在 PAM 中，也拥有 fail 指针，且意义与 AC 自动机的相同，定义 fail[x]fail[x] 为 xx 代表的回文子串的最长回文后缀。

在 trie 树上，我们可以画出所有的 fail 指针。

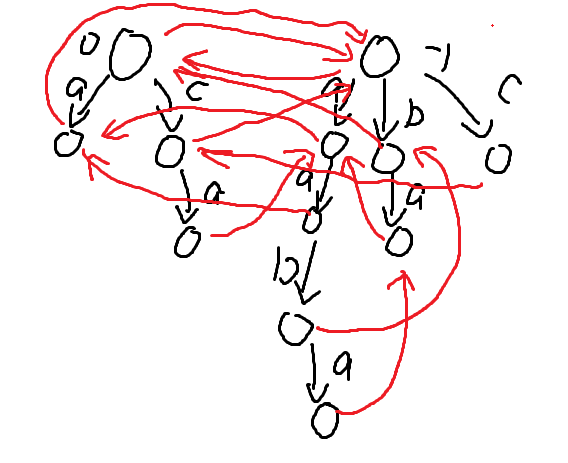
红边为 fail（别吐槽画工了）

我们可以注意到，00 号点的 failfail 指向了 −1-1 号点，这是因为奇根不可能失配（单个字符也是回文串）。

构建

在构建时，我们可以发现：如果我们要插入第 ii 个位置的字符，它会和原字符串的末尾字符形成新的回文串。我们设这个最大回文串的长度为 lenlen。

因为这个串是回文串，因此 s[i−len−1∼i]s[i - len - 1\sim i] 为回文串，两边同时扣掉一个字符，我们就可以发现 s[i−len∼i−1]s[i - len \sim i - 1] 也为回文串。因此我们只需要找一个最长的后缀回文串，满足 s[i−len−1]=s[i]s[i - len - 1] = s[i]，我们就可以把这个字符插入到 s[i−len−1]s[i-len-1] 这个位置所代表的点后。

用图片描述就是：

如何找到这个最长的后缀呢？我们就可以利用 fail 指针。因为我们要找的都是后缀回文串，所以我们可以一直跳 fail，直到 s[i−len−1]s[i-len-1] 和 s[i]s[i] 相等为止。

而新建的这个点的 fail 指针也就可以指向匹配的点（这里也说不清楚），长度就是它父节点加二。

我们在构建时也可以求出一个十分常用的数组 trans，表示长度小于等于当前点的一半的最长回文后缀。

建树代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
inline int getfail(int x, int i)
{
    while(i - len[x] < 1 || s[i - len[x] - 1] != s[i]) x = fail[x];
    return x;
}

inline void build(int n)
{
    len[1] = -1, fail[0] = 1;
    idx = 1;
    for(int i = 1; i <= n; i ++ )
    {
        pos = getfail(cur, i);
        int u = s[i] - 'a';
        if(!tr[pos][u])
        {
            fail[++ idx] = tr[getfail(fail[pos], i)][u];
            tr[pos][u] = idx;
            len[idx] = len[pos] + 2;
            if(len[idx] <= 2) trans[idx] = fail[idx];
            else
            {
                int tmp = trans[cur];
                while(s[i - len[tmp] - 1] != s[i] || ((len[tmp] + 2) << 1) > len[idx])
                    tmp = fail[tmp];
                trans[idx] = tr[tmp][u];
            }
        }
        cur = tr[pos][u];
    }
}

例题

【模板】回文自动机（PAM）

作为模板题，还是比较简单的，统计答案只需要在 fail 指针的基础上加一即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for(int i = 1; i <= n; i ++ )
{
    s[i] = (s[i] - 97 + last) % 26 + 97;
    int pos = getfail(cur, i);
    if(!t[pos][s[i] - 'a'])
    {
        fail[++ idx] = t[getfail(fail[pos], i)][s[i] - 'a'];
        t[pos][s[i] - 'a'] = idx;
        len[idx] = len[pos] + 2;
        num[idx] = num[fail[idx]] + 1;
    }
    cur = t[pos][s[i] - 'a'];
    last = num[cur];
    printf("%d ", last);
}

P3649 [APIO2014] 回文串

本题需要我们统计回文串的出现次数，而当一个回文串出现时，它所对应的 fail 指针所对应的回文串也会出现一次，而它 fail 的 fail 也会出现。而我们如果每次都选择跳 fail，就会导致时间复杂度爆炸。

我们可以按照类似于AC自动机加强版的思路，因为我们插入字符串时是按照拓扑序，所以我们可以先在找到的点上打个标记，最后按照拓扑序向上统计答案即可。

1
2
3
4
5
6
inline void topsort()
{
    for(int i = idx; i >= 0; i -- ) cnt[fail[i]] += cnt[i];
}

for(int i = 0; i <= idx; i ++ ) ans = max(ans, (ll)len[i] * cnt[i]);

P4287 [SHOI2011]双倍回文

本题就用到了我们上面提到的 trans 数组。当一个点的 trans 指向的点的长度恰好为当前点长度的一半时，这个点即为一个双重回文串。

P4762 [CERC2014]Virus synthesis

因为进行一次 2 操作一定优于进行一次 1 操作，因此我们要尽可能的进行 2 操作。

我们设 f[i]f[i] 表示形成在 PAM 中编号为 ii 的点所对应的回文串所需的最小操作次数。我们可以有如下转移：

  1. 在 PAM 上，我们设 xx 扩展出 ii，则当我们将 xx 的一半加上一个字母，再翻折一下，就可以得到 ii 对应的字符串。因此 f[i]=min⁡(f[x]+1,f[i])f[i] = \min (f[x] + 1, f[i])。

  2. 设 transi=ptrans_i = p，我们就可以得到下面的转移方程：f[i]=min⁡(f[i],f[p]+leni2−lenp+1)f[i] = \min(f[i], f[p] + \frac{len_i}{2} - len_p + 1)。

最后统计答案，ans=min⁡{f[i]+n−leni}ans = \min \{ f[i] + n - len_i \}。

我们可以在 bfs 过程中进行状态的转移。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
queue<int> q;
inline void bfs()
{
    while(q.size()) q.pop();
    q.push(0);
    while(q.size())
    {
        int u = q.front();
        q.pop();
        ans = min(ans, f[u] + n - len[u]);
        for(int i = 0; i < 4; i ++ )
        {
            int v = tr[u][i];
            if(!v) continue;
            f[v] = min(f[u] + 1, f[trans[v]] + len[v] / 2 - len[trans[v]] + 1);
            q.push(v);
        }
    }
}

Palindrome Partition

本题将字符串转换一下即可变为一个回文划分问题。

回文划分问题：将字符串 ss 分成 kk 段，使得 s1,s2⋯sks_1, s_2 \cdots s_k 均为回文串。

在本题中，设 fif_i 表示长度为 ii 的前缀的划分方案。于是我们不难得出下面的转移方程：

设谓词 G(x)\mathrm{G(x)} 为 xx 满足回文性质，则

fi=∑G(s[j+1∼i])fjf_i=\sum \limits _{\mathrm{G} (s[j+1\sim i])}f_j

这个转移的复杂度是 O(n2)O(n^2) 的，我们考虑优化。

这里我们再引入两个信息：diff[u]diff[u] 和 slink[u]slink[u]。diff[u]diff[u] 表示该节点和它的 failfail 指针节点的长度差，即为 len[u]−len[fail[u]]len[u] - len[fail[u]]。slink[u]slink[u] 表示 uu 节点一直沿着它的 failfail 指针向上跳，一直跳到第一个满足 diff[x]≠̸diff[u]diff[x] \not\ne diff[u] 的 xx 号点。可以证明，一个节点从 slinkslink 开始跳，跳到根节点的次数不会超过 log⁡∣s∣\log |s| 次。

我们就可以将每一段等差数列中的 ff 值之和存到该等差数列的末端。记为 gg。为了求出这个 gg，我们可以看下图：

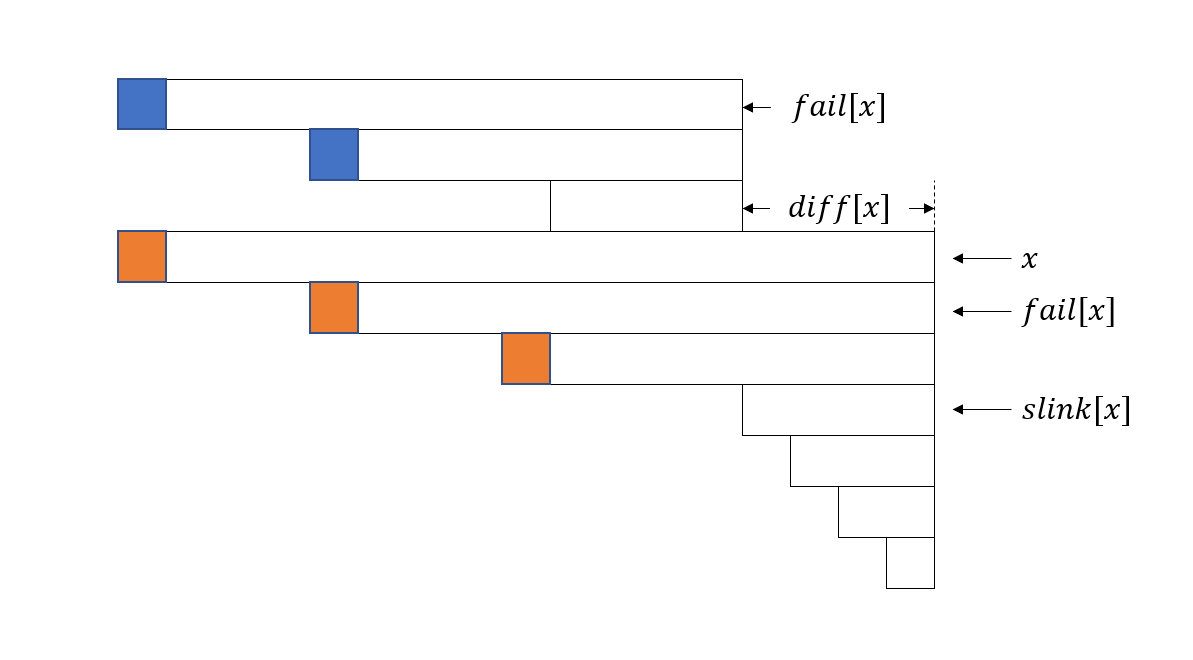
来源：OIwiki

当前跳到了 xx 号节点，我们将要求当前节点的 g[x]g[x]。由于当前回文后缀是回文的，我们可以把它的下一级回文后缀反转到前面，这时我们可以发现它的 fail 的 gg 就存储了等差数列中的一部分值（蓝色部分），我们只差了 f[i−diff[x]−len[slink[x]]]f[i-diff[x]-len[slink[x]]]，我们就可以在跳 slinkslink 的过程中不断更新 ff。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void insert(int i)
{
    pos = getfail(cur, i);
    int u = s[i] - 'a';
    if(!tr[pos][u])
    {
        int x = New(len[pos] + 2);
        fail[x] = tr[getfail(fail[pos], i)][u];
        tr[pos][u] = x;
        diff[x] = len[x] - len[fail[x]];
        if(diff[x] == diff[fail[x]])
            slink[x] = slink[fail[x]];
        else slink[x] = fail[x];
    }
    cur = tr[pos][u];
}

void build(int n)
{
    init();
    f[0] = 1;
    for(int i = 1; i <= n; i ++ )
    {
        insert(i);
        for(int x = cur; x > 1; x = slink[x])
        {
            g[x] = f[i - len[slink[x]] - diff[x]];
            if(diff[x] == diff[fail[x]]) g[x] = add(g[x], g[fail[x]]);
            if((i & 1) == 0) f[i] = add(f[i], g[x]);
        }
    }
}